题目内容
已知tanα=-2，求：
+cos2α的值．
| sinα-2cosα |
| 3sinα+cosα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式利用同角三角函数间的基本关系变形，把已知等式代入计算即可求出值．
解答：
解：∵tanα=-2，
∴原式=
+cos2α=
+
=
+
=
+
=1．
∴原式=
| sinα-2cosα |
| 3sinα+cosβ |
| tanα-2 |
| 3tanα+1 |
| 1 |
| tan2α+1 |
| -2-2 |
| -6+1 |
| 1 |
| 4+1 |
| 4 |
| 5 |
| 1 |
| 5 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
若一个底面是正三角形的三棱柱的主视图如图所示，其顶点都在一个球面上，则该球的表面积（ ）| A、4π | ||
B、
| ||
C、
| ||
D、
|
一批热水器共有98台，其中甲厂生产的有56台，乙厂生产的有42台，用分层抽样从中抽取一个容量为14的样本，那么甲、乙两厂各抽取的热水器的台数是（ ）
| A、9，5 | B、8，6 |
| C、10，4 | D、7，7 |
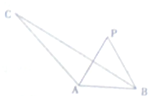如图所示，在△ABC中，∠BAC=120°，AC=3，AB=1，P为∠BAC平分线上异于A的一点，∠APB=α，三角形PAB的面积记为S．