题目内容
已知m、n是两条不同的直线,α、β是两个不同的平面,有下列命题:
①若m?α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若m⊥α,m⊥n,则n∥α;
④若m⊥α,m⊥β,则α∥β;
其中,真命题的个数是( )
①若m?α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若m⊥α,m⊥n,则n∥α;
④若m⊥α,m⊥β,则α∥β;
其中,真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:利用空间线线平行、线面平行、面面平行的性质与判定定理对①②③④四个选项逐一判断即可.
解答:
解:①若m?α,n∥α,则m∥n或m与n异面,故①错误;
②若m∥α,m∥β,则α∥β或α与β相交,故②错误;
③若m⊥α,m⊥n,则n∥α或n?α,故③错误;
④若m⊥α,m⊥β,由线面垂直的性质可知,α∥β,即④正确;
综上所述,真命题的个数是1个.
故选:A.
②若m∥α,m∥β,则α∥β或α与β相交,故②错误;
③若m⊥α,m⊥n,则n∥α或n?α,故③错误;
④若m⊥α,m⊥β,由线面垂直的性质可知,α∥β,即④正确;
综上所述,真命题的个数是1个.
故选:A.
点评:本题考查命题的真假判断与应用,着重考查空间线线平行、线面平行、面面平行的性质与判定,属于中档题.

练习册系列答案
相关题目
已知双曲线中心在原点,且一个焦点为F(3,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-1,则双曲线的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若S={1,2,3,4,5},M={1,3,4},N={2,4,5},则(∁SM)∩(∁SN)等于( )
| A、{1,3} | B、∅ |
| C、{4} | D、{2,5} |
已知复数z1=3+4i,z2=t+i,且z1•
是实数,则t=( )
. |
| z2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设集合A={x|(x+1)(x-5)>0},B={x|a<x<a+8},若A∪B=R,则实数a的取值范围是( )
| A、-3<a<-1 |
| B、-3≤a≤-1 |
| C、a≤-3或a≥-1 |
| D、a<-3或a>-1 |
已知函数f(x)=sinax(a>0)的最小正周期为π,为了得到g(x)=sin(ax+
)的图象,只要将y=f(x)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
 某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5.
某班同学进行了一次数学测试,将所得的数据整理后,画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,且第一小组的频数是5.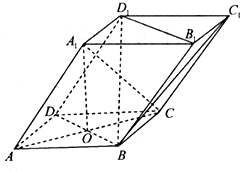 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2