题目内容
7.设全集U={-2,-1,0,1,2},集合M={-1,0,1},N={x|x2-x-2=0},则(∁UM)∩N=( )| A. | {2} | B. | {-1} | C. | {-2,-1,2} | D. | {-1,1} |
分析 直接由全集U,集合M求出∁UM,则N∩(∁UM)的答案可求.
解答 解:∵全集U={-2,-1,0,1,2},集合M={-1,0,1},N={x|x2-x-2=0}={-1,2},
∴∁UM={-2,2}.
则N∩(∁UM)={-1,2}∩{-2,2}={2}.
故选:A.
点评 本题考查了交、并、补集的混合运算,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知等差数列{an}的前n项和为Sn,a1=-7,S8=0.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
15.若复数$\frac{a-3i}{1-2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | -2 | B. | 4 | C. | -6 | D. | 6 |
2.已知命题p;$\frac{1}{2}$≤x≤1,命题q:(x-a)(x-a-1)≤0,若¬p是¬q的必要不充分条件,则实数a的取值范围是( )
| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{3}$,$\frac{1}{2}$] | D. | $(\frac{1}{3},\frac{1}{2}]$ |
12.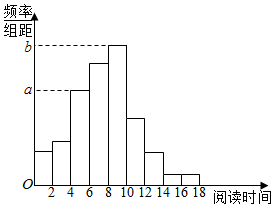 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:| 编号 | 分组 | 频数 |
| 1 | [0,2) | 12 |
| 2 | [2,4) | 16 |
| 3 | [4,6) | 34 |
| 4 | [6,8) | 44 |
| 5 | [8,10) | 50 |
| 6 | [10,12) | 24 |
| 7 | [12,14) | 12 |
| 8 | [14,16) | 4 |
| 9 | [16,18) | 4 |
| 合计 | 200 | |
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
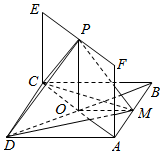 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1. (重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )
(重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )