题目内容
已知过抛物线y2=8x的焦点F的弦AB的中点M，求M到x+2y+4=0的最短距离．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先求M点的轨迹方程，也是抛物线，再平移直线x+2y+4=0与M的轨迹方程相切，切点到直线x+2y+4=0的距离即为所求．
解答：
解：设过抛物线y2=8x的焦点F（2，0）的弦AB的方程为x-2=my，
则x=my+2，代入y2=8x得：y2-8my-16=0，
故弦AB的中点M的综坐标为：
×8m=4m，
代入x=my+2得x=4m2+2，
∴故弦AB的中点M的坐标为：（4m2+2，4m），
故弦AB的中点M的轨迹方程为：y2=4（x-2），
令x+2y+c=0与y2=4（x-2）相切，
则y2=-4（2y+c+2），即y2+8y+4c+8=0的△=64-16c-32=0，
解得c=2，
联立
得：
由（6，-4）到x+2y+4=0的距离d=
=
，
可得M到x+2y+4=0的最短距离为
．
则x=my+2，代入y2=8x得：y2-8my-16=0，
故弦AB的中点M的综坐标为：
| 1 |
| 2 |
代入x=my+2得x=4m2+2，
∴故弦AB的中点M的坐标为：（4m2+2，4m），
故弦AB的中点M的轨迹方程为：y2=4（x-2），
令x+2y+c=0与y2=4（x-2）相切，
则y2=-4（2y+c+2），即y2+8y+4c+8=0的△=64-16c-32=0，
解得c=2，
联立
|
|
由（6，-4）到x+2y+4=0的距离d=
| |6-4×2+4| | ||
|
2
| ||
| 5 |
可得M到x+2y+4=0的最短距离为
2
| ||
| 5 |
点评：本题考查的知识点是抛物线的简单性质，直线与圆锥曲线的关系，点到直线的距离，难度中档．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
已知集合M={x||x|＜2}，N={x|-1≤x≤3}，M∪N=（ ）
| A、{-1，2} |
| B、[-1，2） |
| C、{-2，3} |
| D、（-2，3] |
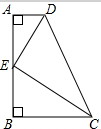如图，在直角梯形ABCD中，AB⊥AD，AB⊥BC，∠BCD与∠ADC的平分线相交于AB上的一点E，以AB为直径作圆，则该圆与边DC有怎样的位置关系？请说明理由．