题目内容
18.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2$\sqrt{2}$,|$\overrightarrow{a}$-$\overline{b}$|=2,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为( )| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{{5\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
分析 由条件利用两个向量的数量积的定义,求得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2$\sqrt{2}$,再根据|$\overrightarrow{a}$-$\overline{b}$|=2=$\sqrt{{(\overrightarrow{a}-\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{1-2\overrightarrow{a}•\overrightarrow{b}+8}$,
∴$a•b=\frac{5}{2}$,
则则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{5\sqrt{2}}{8}$,
故选:C.
点评 本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
6.若$\frac{1+2i}{a+bi}=1+i$,其中a、b为实数,则a+b的值等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
13.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6},则A∪(∁UB)=( )
| A. | {2,5} | B. | {2,5,7,8} | C. | {2,3,5,6,7,8} | D. | {1,2,3,4,5,6} |
3.执行图中程序框图,如果输入x1=2,x2=3,x3=7,则输出的T值为( )


| A. | 0 | B. | 4 | C. | 2 | D. | 3 |
10.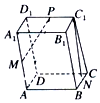 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
7.已知函数f(x)=-3lnx+ax2+bx(a>0,b∈R),若对任意x>0都有f(x)≥f(3)成立,则( )
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna≤-b-1 | D. | lna<-b-1 |