题目内容
已知函数f（x）=x|x-4|（x∈R），若存在正实数k，使得方程f（x）=k有两个根a、b，其中2＜a＜b，则ab-2（a+b）的取值范围是（ ）
A、（2，2+2
| ||
| B、（-4，0） | ||
| C、（-2，2） | ||
| D、（-4，2） |
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：先分别求出a，b，再代入计算，即可确定ab-2（a+b）的取值范围．
解答：
解：当x＞4时，x2-4x-k=0，∴b=2+
；
当x＜4时，x2-4x+k=0，∴a=2+
，且0＜k＜4，
由ab-2（a+b）=-4+
，0＜k＜4 得到-4＜ab-2（a+b）＜0，
故选：B．
| 4+k |
当x＜4时，x2-4x+k=0，∴a=2+
| 4-k |
由ab-2（a+b）=-4+
| 16-k2 |
故选：B．
点评：本题考查ab-2（a+b）的取值范围，解题的关键是求出a，b．
练习册系列答案
相关题目
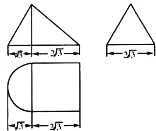一个几何体的三视图如图所示，且其左视图是一个等边三角形，则这个几何体的体积为（ ）A、12+
| ||
B、36+
| ||
C、18+
| ||
D、6+
|