题目内容
8.已知函数$f(x)=2+\frac{4}{x},g(x)={2^x}$.(1)设函数h(x)=g(x)-f(x),求函数h(x)在区间[2,4]上的值域;
(2)定义min(p,q)表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0),
①求函数H(x)的单调区间及最值;
②若关于x的方程H(x)=k有两个不同的实根,求实数k的取值范围.
分析 (1)根据函数f(x),g(x)的单调性,求出h(x)的单调性,求出函数h(x)的值域即可;
(2)①根据函数f(x),g(x)的图象求出H(x)的最大值,②根据H(x)的范围,求出k的范围即可.
解答 解:(1)∵函数f(x)在区间(0,+∞)上单调递减,
函数g(x)在区间(0,+∞)上单调递增,
∴函数h(x)在区间[2,4]上单调递增,
故h(2)≤h(x)≤h(4),即0≤h(x)≤13,
所以函数在区间[2,4]上的值域为[0,13].…(4分)
(2)①在同一坐标系中,作出f(x),g(x)的图象如图所示,
根据题意得,H(x)=$\left\{\begin{array}{l}{{2}^{x},0<x≤2}\\{2+\frac{4}{x},x>2}\end{array}\right.$,
由(1)知,y=2x在区间(0,2]上单调递增,
$y=2+\frac{4}{x}$在区间上单调递减,
故H(x)max=H(2)=4.
∴函数H(x)的单调递增区间为(0,2],单调递减区间为(2,+∞),
H(x)有最大值4,无最小值.…••(8分)
②∵$f(x)=2+\frac{4}{x}$在[2,+∞)上单调递减,∴$2<2+\frac{4}{x}≤4$,
又g(x)=2x在(0,2]上单调递增,∴1<2x≤4,
∴要使方程H(x)=k有两个不同的实根,
则需满足2<k<4,
即实数k的取值范围是(2,4).…(12分)
点评 本题考查了函数的单调性、值域问题,考查导数的应用以及数形结合思想,是一道中档题.

练习册系列答案
相关题目
16.全称命题“?x∈R,x2+5x=4”的否定是( )
| A. | $?{x_0}∈R,{x_0}^2+5{x_0}=4$ | B. | ?x∈R,x2+5x≠4 | ||
| C. | $?{x_0}∈R,{x_0}^2+5{x_0}≠4$ | D. | 以上都不正确 |
3.圆x2+y2+2ax+4ay=0的半径为$\sqrt{5}$,则a等于( )
| A. | 5 | B. | -5或5 | C. | 1 | D. | 1或-1 |
20.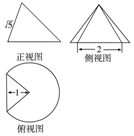 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )| A. | $π+\frac{2}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{3}{4}π+\frac{2}{3}$ | D. | $\frac{3}{4}π+\frac{1}{3}$ |
17.定义在R上的函数y=f(x)满足:f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)-ex>2016(其中e为自然对数的底数)的解集为( )
| A. | (2016,+∞) | B. | (-∞,0)∪(2016,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (0,+∞) |
18.已知点(x,y)满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$,则$z=\frac{y}{x+1}$的最小值为( )
| A. | 3 | B. | $\frac{7}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
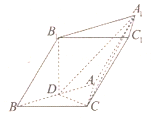 如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.
如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.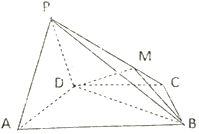 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.