题目内容
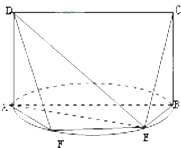 如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在平面,且AB=2AD=2.
如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在平面,且AB=2AD=2.(Ⅰ)求证:EA⊥EC;
(Ⅱ)设平面ECD与半圆弧的另一个交点为F,
①求证:EF∥AB;
②若EF=1,求多面体ABCDEF的体积V.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)利用面面垂直的性质,可得BC⊥平面ABE,再利用线面垂直的判定证明AE⊥面BCE,即可证得结论;
(Ⅱ)①先证明AB∥面CED,再利用线面平行的性质,即可证得结论;
②分别取AB、EF的中点为O、M,连接OM,利用V=VD-AEF+VE-ABCD,可得结论.
(Ⅱ)①先证明AB∥面CED,再利用线面平行的性质,即可证得结论;
②分别取AB、EF的中点为O、M,连接OM,利用V=VD-AEF+VE-ABCD,可得结论.
解答:
(Ⅰ)证明:∵E是半圆上异于A、B的点,∴AE⊥EB,
又∵矩形平面ABCD⊥平面ABE,且CB⊥AB,
由面面垂直性质定理得:CB⊥平面ABE,∴平面CBE⊥平面ABE,
且二面交线为EB,由面面垂直性质定理得:AE⊥平面CBE,
又EC在平面CBE内,故得:EA⊥EC…(4分)
(Ⅱ①证明:由CD∥AB,得CD∥平面ABE,
又∵平面CDE∩平面ABE于直线EF,
∴根据线面平行的性质定理得:CD∥EF,CD∥AB,故EF∥AB …(7分)
②解:分别取AB、EF的中点为O、M,连接OM,则在直角三角形OME中,OM=
,
∵矩形ABCD所在的平面垂直于该半圆所在平面,OM⊥AB,
∴OM⊥平面ABCD,即OM为M到面ABCD之距,
又∵EF∥AB,∴E到到面ABCD之距也为OM=
,…(9分)
∴V=VD-AEF+VE-ABCD=
×
×1×
×1+
×2×1×
=
…(12分)
又∵矩形平面ABCD⊥平面ABE,且CB⊥AB,
由面面垂直性质定理得:CB⊥平面ABE,∴平面CBE⊥平面ABE,
且二面交线为EB,由面面垂直性质定理得:AE⊥平面CBE,
又EC在平面CBE内,故得:EA⊥EC…(4分)
(Ⅱ①证明:由CD∥AB,得CD∥平面ABE,
又∵平面CDE∩平面ABE于直线EF,
∴根据线面平行的性质定理得:CD∥EF,CD∥AB,故EF∥AB …(7分)
②解:分别取AB、EF的中点为O、M,连接OM,则在直角三角形OME中,OM=
| ||
| 2 |
∵矩形ABCD所在的平面垂直于该半圆所在平面,OM⊥AB,
∴OM⊥平面ABCD,即OM为M到面ABCD之距,
又∵EF∥AB,∴E到到面ABCD之距也为OM=
| ||
| 2 |
∴V=VD-AEF+VE-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
5
| ||
| 12 |
点评:本题考查面面垂直的性质,线面垂直的判定与性质,考查线面垂直,考查体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 用三种不同的颜色填涂如图中的6个区域,要求每行、每列的区域都不同色,则不同的填涂方法种数共有( )
用三种不同的颜色填涂如图中的6个区域,要求每行、每列的区域都不同色,则不同的填涂方法种数共有( )| A、12 | B、24 | C、12 | D、6 |
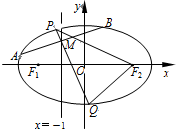 如图,F1、F2是离心率为
如图,F1、F2是离心率为