��Ŀ����
9����֪ij��ѧ�����Ŀư�ѧ������800�˲μ�����ѧ�������ˮƽ���ԣ�ѧУ��������������������г�ȡ100�˽��гɼ��������飬�Ƚ�800�˰�001��002������800���б�ţ���1������ӵ�8�е�7�е�����ʼ���Ҷ�����������д�����ȼ���3���˵ı�ţ�
������ժȡ�˵�7�е���9�У�

��2����ȡ��100�˵���ѧ�������ˮƽ���Գɼ����±���
�ɼ���Ϊ���㡢���á����������ȼ�����������ֱ��ʾ�����ɼ�����ѧ�ɼ������磺������ѧ�ɼ�Ϊ���õĹ���20+18+4=42��
�����ڸ������У���ѧ�ɼ���������30%����a��b��ֵ��
| ���� | ��ѧ | |||
| ���� | ���� | ���� | ||
| ���� | ���� | 7 | 20 | 5 |
| ���� | 9 | 18 | 6 | |
| ���� | a | 4 | b | |
���� ��1���������������������д�����ȼ���3���˵ı�ţ�
��2�����ڸ������У�����ѧ�ɼ���������30%�������a��b��ֵ��
��a+b=31��a��11��b��7�������оٷ��������ѧ�ɼ�����������ȼ���������ٵĸ��ʣ�
��� �⣺��1������������������г�ȡ100�˽��гɼ��������飬
�Ƚ�800�˰�001��002������800���б�ţ�
�ӵ�8�е�7�е�����ʼ���Ҷ�������д�����ȼ���3���˵ı��Ϊ��
785��667��199
��2���١��ڸ������У���ѧ�ɼ���������30%��
��$\frac{7+9+a}{100}$=30%����a=14��
b=100-30-��20+18+4��-��5+6��=17��
��a+b=100-��7+20+5��-��9+18+6��-4=31��
��a��11��b��7����a��b�Ĵ��䣬
��11��20������12��19������13��18������14��17������15��16������16��15������17��14������18��13������19��12����
��20��11������21��10������22��9������23��8������24��7��������14�֣�
��a��11��b��7����ѧ�ɼ�����������ȼ����������Ϊ�¼�A��a+5��b��
�¼�A��������11��20������12��19������2�������¼���
P��A��=$\frac{2}{14}=\frac{1}{7}$����ѧ�ɼ�����������ȼ���������ٵĸ���Ϊ$\frac{2}{14}=\frac{1}{7}$��
���� ���⿼�����������Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�

 �߽�������ϵ�д�
�߽�������ϵ�д�| A�� | 15��ܦȡ�90�� | B�� | 60��ܦȡ�90�� | C�� | 15��ܦȡ�105�� | D�� | 30��ܦȡ�105�� |
| A�� | ��2��+�ޣ� | B�� | ��2��6�� | C�� | ��0��6�� | D�� | ��0��2�� |
| A�� | 9 | B�� | 3 | C�� | $\frac{{3\sqrt{2}}}{2}$ | D�� | 9$\sqrt{2}$ |

| A�� | {x|x��1} | B�� | {x|1��x��2} | C�� | {x|x��2} | D�� | {x|x��2} |
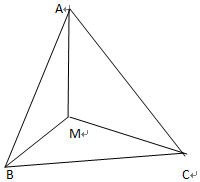 ��ͼ���ȱߡ�ABC�У�AB=2��MΪ��ABC��һ���㣬��BMC=120�㣻
��ͼ���ȱߡ�ABC�У�AB=2��MΪ��ABC��һ���㣬��BMC=120�㣻