题目内容
设函数f(x)=lnx+
ax2-ax.
(1)若函数f(x)在x=2处取得极值,求a的值,并求出此时函数的单调区间;
(2)若函数f(x)>0对x∈[1,2]恒成立,求a的取值范围.
| 1 |
| 2 |
(1)若函数f(x)在x=2处取得极值,求a的值,并求出此时函数的单调区间;
(2)若函数f(x)>0对x∈[1,2]恒成立,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)将x=2代入导函数求出a的值,再将a=-
代入导函数求出x的值,从而求出单调区间;
(2)由函数在[1,2]上递增,得到f(1)最小,由f(1)>0解得即可.
| 1 |
| 2 |
(2)由函数在[1,2]上递增,得到f(1)最小,由f(1)>0解得即可.
解答:
解:(1)∵f′(x)=
+ax-a,
∴f′(2)=
+2a-a=0,
解得:a=-
,
∴f′(x)=
-
x+
=0,
解得:x=-1(舍),x=2,
∴f(x)在(0,2)递增,在(2,+∞)递减;
(2)由(1)得:f(x)在[1,2]上单调递增,
∴f(x)min=f(1)=
a-a>0,
解得:a<0,
∴a的范围是:(-∞,0).
| 1 |
| x |
∴f′(2)=
| 1 |
| 2 |
解得:a=-
| 1 |
| 2 |
∴f′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=-1(舍),x=2,
∴f(x)在(0,2)递增,在(2,+∞)递减;
(2)由(1)得:f(x)在[1,2]上单调递增,
∴f(x)min=f(1)=
| 1 |
| 2 |
解得:a<0,
∴a的范围是:(-∞,0).
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
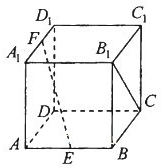 如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.