题目内容
18.计算:sin(-$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,cos(-$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,tan(-$\frac{7π}{6}$)=$-\frac{\sqrt{3}}{3}$.分析 利用诱导公式以及特殊角的三角函数化简求解即可.
解答 解:sin(-$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,cos(-$\frac{π}{6}$)=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,tan(-$\frac{7π}{6}$)=-tan$\frac{π}{6}$=-$\frac{\sqrt{3}}{3}$.
故答案为:-$\frac{\sqrt{2}}{2}$;$\frac{\sqrt{3}}{2}$;$-\frac{\sqrt{3}}{3}$.
点评 本题考查特殊角的三角函数,诱导公式的应用,考查计算能力.

练习册系列答案
相关题目
8.已知|$\overrightarrow a$|=4cos$\frac{π}{8}$,|$\overrightarrow b$|=2sin$\frac{π}{8}$,$\overrightarrow a$•$\overrightarrow b$=-$\sqrt{2}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
9.设a=log0.32,b=ln2,c=5${\;}^{\frac{1}{2}}}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
6.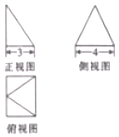 某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )
某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )
 某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )
某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 16 |
13.在区间[-2,2]上随机取一个数x,使得|x+1|+|x-1|≤3成立的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
3.命题“?x0∈(0,+∞),ln x0=x0-1”的否定是( )
| A. | ?x∈(0,+∞),ln x≠x-1 | B. | ?x∉(0,+∞),ln x=x-1 | ||
| C. | ?x0∈(0,+∞),ln x0≠x0-1 | D. | ?x0∉(0,+∞),ln x0=x0-1 |
7.当圆锥的侧面积和底面积的比值是2时,圆锥轴截面的顶角等于( )
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |