当圆锥的侧面积和底面积的比值是2时.圆锥轴截面的顶角等于( )A．45°B．60°C．90°D．120° 题目和参考答案——青夏教育精英家教网—

题目内容

7．当圆锥的侧面积和底面积的比值是2时，圆锥轴截面的顶角等于（　　）

A．

45°

B．

60°

C．

90°

D．

120°

分析设圆锥的母线长为l，底面半径为r，得出$\frac{l}{r}$=2，利用中截面三角形求解即可．

解答解：设圆锥的母线长为l，底面半径为r，
则$\frac{πrl}{π{r}^{2}}$=2，∴$\frac{l}{r}$=2，
设轴截面顶角的一半为α，
则sinα=$\frac{r}{l}$=$\frac{1}{2}$，∴α=30°，2α=60°．
故选B

点评本题考查圆锥的结构特征，基本几何量的计算．属于基础题．

练习册系列答案

18．计算：sin（-$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$，cos（-$\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$，tan（-$\frac{7π}{6}$）=$-\frac{\sqrt{3}}{3}$．

15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≥0}\\{4x-{x}^{2}，x＜0}\end{array}\right.$，若f（3-2a）＞f（a），则实数a的取值范围是（-∞，1）．

2．已知函数$f（x）=x+\frac{2}{x}$，利用定义证明：
（1）f（x）为奇函数；
（2）f（x）在$[\sqrt{2}$，+∞）上是增加的．

12．

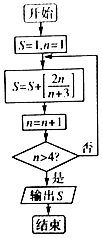若[x]表示不超过x的最大整数，如[2，6]=2，[-2，6]=-3，执行如图所示的程序框图，记输出的值为S₀，则${log_{\frac{1}{3}}}{S_0}$=（　　）

19．f（x）=xsinx+cosx；
（1）判断f（x）在区间（2，3）上的零点个数，并证明你的结论（参考数据：$\sqrt{2}≈1.4，\sqrt{6}$≈2.4）
（2）若存在$x∈（{\frac{π}{4}，\frac{π}{2}}）$，使得f（x）＞kx²+cosx成立，求实数k的取值范围．

16．函数f（x）=$\left\{\begin{array}{l}{（x-a）^2}+1，x≤0\\{x^2}+\frac{2}{x}+a，x＞0\end{array}$，若f（0）是f（x）的最小值，则a的取值范围为（　　）

17．已知角的终边过点P（-1，2），则cosα的值为-$\frac{\sqrt{5}}{5}$．

试题分类