某几何体的三视图如图所示.其侧视图是一个等边三角形.则此几何体的体积是( )A．24$\sqrt{3}$B．8$\sqrt{3}$C．16$\sqrt{3}$D．16 题目和参考答案——青夏教育精英家教网—

题目内容

6．

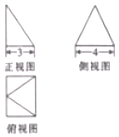某几何体的三视图如图所示，其侧视图是一个等边三角形，则此几何体的体积是（　　）

A．

24$\sqrt{3}$

B．

8$\sqrt{3}$

C．

16$\sqrt{3}$

D．

分析根据三视图可知该几何体是四棱锥，底面是长为4，宽为3的矩形．高为2$\sqrt{3}$．可得此几何体的体积．

解答解：由题意：该几何体是四棱锥，底面是长为4，宽为3的矩形．
侧视图是一个等边三角形，所以高为2$\sqrt{3}$．
此几何体的体积$V=\frac{1}{3}Sh$=4×3×$\frac{1}{3}×2\sqrt{3}$=8$\sqrt{3}$．
故选：B．

点评本题考查了对三视图的投影认识和理解，边长之间的关系以及棱锥体的体积计算．

练习册系列答案

新编高中假期作业四川师范大学电子出版社系列答案

授之以渔中考复习方案系列答案

中考提分攻略系列答案

寒假天地寒假作业本延边大学出版社系列答案

相关题目

16．设集合A={x∈N|0≤x＜3}的真子集个数为（　　）

17．已知函数f（x）=$\left\{\begin{array}{l}{log_2}（1-x），x＜1\\-{（x-2）^2}+2，x≥1\end{array}$，则关于x的方程f（|x|）=a（a∈R）的实根个数不可能为（　　）

14．直线l：y=x+1上的点到圆C：x²+y²+2x+4y+4=0上的点的最近距离为（　　）

1．f（x）=$\sqrt{2}$cos（2x-$\frac{π}{4}$）．
（1）求f（x）的对称轴和对称中心；
（2）求函数f（x）在[-$\frac{π}{8}$，$\frac{π}{2}$]上的最小值和最大值，并求出取得最值时的x值．

11．命题“若a+b+c=3，则a²+b²+c²≥3”的逆命题是（　　）

	A．	“若a²+b²+c²≥3，则a+b+c=3”		B．	“若a²+b²+c²＜3，则a+b+c≠3”
	C．	“若a²+b²+c²≥3，则a+b+c≠3”		D．	“若a²+b²+c²＜3，则a+b+c=3”

18．计算：sin（-$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$，cos（-$\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$，tan（-$\frac{7π}{6}$）=$-\frac{\sqrt{3}}{3}$．

15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≥0}\\{4x-{x}^{2}，x＜0}\end{array}\right.$，若f（3-2a）＞f（a），则实数a的取值范围是（-∞，1）．

16．函数f（x）=$\left\{\begin{array}{l}{（x-a）^2}+1，x≤0\\{x^2}+\frac{2}{x}+a，x＞0\end{array}$，若f（0）是f（x）的最小值，则a的取值范围为（　　）

试题分类