题目内容
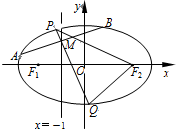 如图,F1、F2是离心率为
如图,F1、F2是离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
| F2P |
| F2Q |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ) 设F2(c,0),则
=
,离心率e=
,由此能求出椭圆C的方程.
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-1,
•
=-4.当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-1,m) (m≠0),A(x1,y1),B(x2,y2).利用点差法求出PQ的直线方程为y=-2mx-m.联立
,得:(8m2+1)x2+8m2x+2m2-8=0.由此能求出
•
的取值范围是[-4,
).
| c-1 |
| c+1 |
| 1 |
| 3 |
| ||
| 2 |
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-1,
| F2P |
| F2Q |
|
| F2P |
| F2Q |
| 125 |
| 58 |
解答:
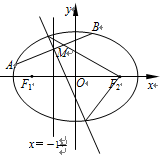 解:(Ⅰ) 设F2(c,0),则
解:(Ⅰ) 设F2(c,0),则
=
,
解得c=2.
∵离心率e=
,∴a=2
.
∴椭圆C的方程为
+
=1.…(6分)
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-1,
此时P(-2
,0)、Q(2
,0),
•
=-4.
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-1,m) (m≠0),
A(x1,y1),B(x2,y2).
由
,得(x1+x2)+2(y1+y2)•
=0,
则-1+2mk=0,故k=
.…(8分)
此时,直线PQ斜率为k1=-2m,
PQ的直线方程为y-m=-2m(x+1).即y=-2mx-m.
联立
,消去y,整理得:
(8m2+1)x2+8m2x+2m2-8=0.
∴x1+x2=-
,x1x2=
.…(10分)
∴
•
=(x1-2)(x2-2)+y1y2
=x1x2-2(x1+x2)+1+(2mx1+m)(2mx2+m)
=(1+4m2)x1x2+(2m2-2)(x1+x2)+4+m2
=
.
令t=1+8m2,1<t<29,
则
•
=
-
,
又1<t<29,∴-4<
•
<
,
综上,
•
的取值范围是[-4,
).…(14分)
 解:(Ⅰ) 设F2(c,0),则
解:(Ⅰ) 设F2(c,0),则| c-1 |
| c+1 |
| 1 |
| 3 |
解得c=2.
∵离心率e=
| ||
| 2 |
| 2 |
∴椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-1,
此时P(-2
| 2 |
| 2 |
| F2P |
| F2Q |
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-1,m) (m≠0),
A(x1,y1),B(x2,y2).
由
|
| y1-y2 |
| x1-x2 |
则-1+2mk=0,故k=
| 1 |
| 2m |
此时,直线PQ斜率为k1=-2m,
PQ的直线方程为y-m=-2m(x+1).即y=-2mx-m.
联立
|
(8m2+1)x2+8m2x+2m2-8=0.
∴x1+x2=-
| 8m2 |
| 8m2+1 |
| 2m2-8 |
| 8m2+1 |
∴
| F2P |
| F2Q |
=x1x2-2(x1+x2)+1+(2mx1+m)(2mx2+m)
=(1+4m2)x1x2+(2m2-2)(x1+x2)+4+m2
=
| 19m2-4 |
| 8m2+1 |
令t=1+8m2,1<t<29,
则
| F2P |
| F2Q |
| 19 |
| 8 |
| 51 |
| 8t |
又1<t<29,∴-4<
| F2P |
| F2Q |
| 125 |
| 58 |
综上,
| F2P |
| F2Q |
| 125 |
| 58 |
点评:本题考查椭圆方程的求法,考查向量的数量积的取值范围的求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
经过点(0,-2)且在两坐标轴上截距和为2的直线方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=㏑(x-1)在区间(1,+∞)内是( )
| A、单调递增 | B、单调递减 |
| C、有极小值 | D、有极大值 |
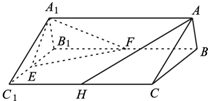 如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.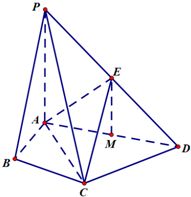 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.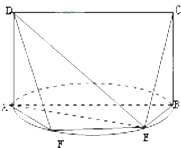 如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在平面,且AB=2AD=2.
如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在平面,且AB=2AD=2.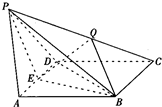 已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=
已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=