题目内容
已知函数f(x)=(sin2x+cos2x)2-2sin22x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)当x∈[-
,
]时,求y=f(x)的值域.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)当x∈[-
| π |
| 8 |
| π |
| 8 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角的正弦、余弦公式、两角和与差的正弦公式化简函数解析式,化为一个角的正弦函数,由最小正周期公式求解;
(Ⅱ)由x的范围求出4x+
的范围,再由正弦函数得性质求出f(x)的最值,再求出函数f(x)的值域.
(Ⅱ)由x的范围求出4x+
| π |
| 4 |
解答:
解:(I)f(x)=(sin2x+cos2x)2-2sin22x=1+2sin2xcos2x-(1-cos4x)
=sin4x+cos4x=
sin(4x+
),
∴T=
=
,
则f(x)的最小正周期是
,
(II)由(I)得f(x)=
sin(4x+
),
∵x∈[-
,
],∴4x+
∈[-
,
],
当4x+
=-
时,此时x=-
,f(x)min=
×(-
)=-1,
当4x+
=
时,此时x=
,f(x)m,ax=
,
则f(x)的值域是[-1,
].
=sin4x+cos4x=
| 2 |
| π |
| 4 |
∴T=
| 2π |
| 4 |
| π |
| 2 |
则f(x)的最小正周期是
| π |
| 2 |
(II)由(I)得f(x)=
| 2 |
| π |
| 4 |
∵x∈[-
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
当4x+
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 2 |
| ||
| 2 |
当4x+
| π |
| 4 |
| π |
| 2 |
| π |
| 16 |
| 2 |
则f(x)的值域是[-1,
| 2 |
点评:本题考查二倍角的正弦、余弦公式、两角和与差的正弦公式,以及正弦函数的性质,熟练掌握公式及性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
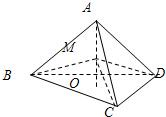 如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.
如图,已知AO是四面体ABCD的高,M是AO的中点,连接BM、CM、DM.求证:BM、CM、DM两两垂直.