题目内容
已知抛物线y2=2px(p>0),抛物线上纵坐标为1的点到焦点的距离为p,过点M(1,0)作斜率为k的直线l交抛物线于A,B两点,A点关于x轴的对称点为C,直线BC交x轴于Q点.
(Ⅰ)求p的值;
(Ⅱ)探究:当k变化时,点Q是否为定点?
(Ⅰ)求p的值;
(Ⅱ)探究:当k变化时,点Q是否为定点?
考点:直线与圆锥曲线的关系,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)首先设抛物线y2=2px(p>0)上纵坐标为1的点为N,则N(
,1);然后根据抛物线的定义,列出关于p的方程,求解即可;
(2)由(1),可得抛物线方程为:y2=2x,设过点M(1,0)做斜率为k的直线l的方程为:y=k(x-1),将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,然后根据根与系数的关系,即可求出点Q的坐标.
| 1 |
| 2p |
(2)由(1),可得抛物线方程为:y2=2x,设过点M(1,0)做斜率为k的直线l的方程为:y=k(x-1),将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,然后根据根与系数的关系,即可求出点Q的坐标.
解答:
解:(1)设抛物线y2=2px(p>0)上纵坐标为1的点为N,则N(
,1),
根据题意,N(
,1)在抛物线上,
则
+
=p,可得p=1;
(2)过点M(1,0)做斜率为k的直线l的方程为:y=k(x-1),
设A(
,y1),B(
,y2),
则C(
,-y1),kBC=
=
,
所以直线BC的方程为:y+y1=
(x-
),
因此当y=0时,x=
,即Q(
,0),
又因为
,
可得ky2-2y-2k=0,则y1y2=-2,
所以当k变化时,点Q为定点,其坐标为(-1,0).
| 1 |
| 2p |
根据题意,N(
| 1 |
| 2p |
则
| 1 |
| 2p |
| p |
| 2 |
(2)过点M(1,0)做斜率为k的直线l的方程为:y=k(x-1),
设A(
| y12 |
| 2 |
| y22 |
| 2 |
则C(
| y12 |
| 2 |
| y2+y1 | ||||
|
| 2 |
| y2-y1 |
所以直线BC的方程为:y+y1=
| 2 |
| y2-y1 |
| y12 |
| 2 |
因此当y=0时,x=
| y1y2 |
| 2 |
| y1y2 |
| 2 |
又因为
|
可得ky2-2y-2k=0,则y1y2=-2,
所以当k变化时,点Q为定点,其坐标为(-1,0).
点评:本题主要考查了直线与圆锥曲线的综合应用,考查了抛物线的定义、轨迹方程的求法,还考查了等价转化的思想,属于中档题.

练习册系列答案
相关题目
已知x1,x2分别是函数f(x)=log2x-(
)x和g(x)=log
x-(
)x的零点,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、x1x2<0 |
| B、0<x1x2<1 |
| C、x1x2=1 |
| D、1<x1x2<2 |
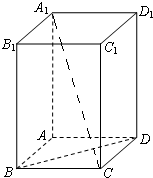 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
 如图所示,四棱锥P-ABCD中,底面ABCD是个边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是个边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.