题目内容
一块橡皮1元钱，一枝笔2元钱，问100元钱能买橡皮和笔各多少？
数学模型：设能买橡皮X块，笔Y枝，则X+2Y=100．求此方程的正整数解．
设计一个求此问题的算法，画出流程图并用伪代码表示．
数学模型：设能买橡皮X块，笔Y枝，则X+2Y=100．求此方程的正整数解．
设计一个求此问题的算法，画出流程图并用伪代码表示．
考点：设计程序框图解决实际问题,伪代码
专题：应用题,算法和程序框图
分析：本题考查的知识点是设计程序框图解决实际问题，我们根据题意即可确定算法，画出流程图，再编写满足题意的程序．
解答：
解：伪代码如下：
Begin
For Y from 1 to 49
X=100-2Y
Print X，Y
End for
End
流程图如下：
Begin
For Y from 1 to 49
X=100-2Y
Print X，Y
End for
End
流程图如下：
点评：本题考查了设计程序框图解决实际问题，主要考查编写伪代码程序解决实际问题，属于中档题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
P是椭圆
+
=1（a＞b＞0）上的一个点，F为该椭圆的左焦点，O为坐标原点，且△POF为正三角形．则该椭圆离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||||
B、2-
| ||||
C、
| ||||
D、
|
函数f（x）=x-a+log2x存在大于1的零点，则a的取值范围是（ ）
| A、[1，∞） |
| B、（1，+∞） |
| C、（0，+∞） |
| D、（-∞，1） |
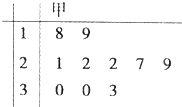某篮球运动员甲参加了10场比赛，他每场比赛得分的茎叶图如图所示，则数据落在区间[22，30）内的概率为（ ）
| A、0.6 | B、0.5 |
| C、0.4 | D、0.3 |
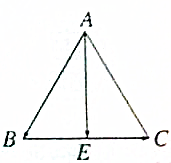如图，已知△ABC是等边三角形．