题目内容
已知f(x-1)的定义域为[-3,3],则f(x)定义域为 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:f(x-1)的定义域为[-3,3],是指的x的范围是[-3,3],由此求出x-1的范围得到f(x)的定义域.
解答:
解:∵f(x-1)的定义域为[-3,3],即-3≤x≤1.
∴-4≤x-1≤2,
即函数f(x)定义域为[-4,2].
故答案为:[-4,2].
∴-4≤x-1≤2,
即函数f(x)定义域为[-4,2].
故答案为:[-4,2].
点评:本题考查了与抽象函数有关的简单复合函数定义域的求法,关键是对该类问题求解方法的掌握,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则一定成立的是( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)>f(cosB) |
若函数f(x)=ex(x≤0)的反函数为y=f-1(x),则函数y=f-1(2x-1)的定义域为( )
| A、(0,1] | ||
| B、(-1,1] | ||
C、(-∞,
| ||
D、(
|
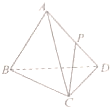 如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.
如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.