题目内容
已知以F1(-2,0),F2(2,0)为焦点的椭圆与直线x+
y+4=0有且仅有一个交点,求椭圆的方程.
| 3 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设椭圆的标准方程为
+
=1,(a>b>0).与直线方程联立化为(a2+3b2)y2+8
b2y+16b2-a2b2=0,
由于椭圆与直线x+
y+4=0有且仅有一个交点,可得△=0,又a2=b2+4,联立解得即可.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
由于椭圆与直线x+
| 3 |
解答:
解:设椭圆的标准方程为
+
=1,(a>b>0).
联立
,化为(a2+3b2)y2+8
b2y+16b2-a2b2=0,
∵椭圆与直线x+
y+4=0有且仅有一个交点,
∴△=0,化为a2+3b2=16,
又a2=b2+4,联立
,解得
.
∴椭圆的标准方程为:
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
联立
|
| 3 |
∵椭圆与直线x+
| 3 |
∴△=0,化为a2+3b2=16,
又a2=b2+4,联立
|
|
∴椭圆的标准方程为:
| x2 |
| 7 |
| y2 |
| 3 |
点评:本题考查了椭圆的标准方程及其性质,考查了直线与椭圆相切问题转化为方程联立可得△=0,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若a>0,b>0,c>0,a+b>c,则( )
| x |
| x+1 |
| A、f(a)+f(b)>f(c) |
| B、f(a)+f(b)=f(c) |
| C、f(a)+f(b)<f(c) |
| D、以上结论都不对 |
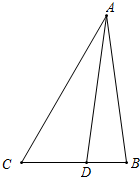 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2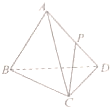 如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.
如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.