题目内容
已知函数f(x)是奇函数,当x>0时,f(x)=ax(a>0,a≠1),且f(log
4)=-
,则a的值为( )
| 1 |
| 2 |
| 9 |
| 4 |
A、
| ||
| B、3 | ||
| C、9 | ||
D、
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由于函数f(x)是奇函数,可得-
=f(log
4)=f(-2)=-f(2),再利用当x>0时,f(x)=ax(a>0,a≠1),可得a2=
,解得a即可.
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
解答:
解:∵函数f(x)是奇函数,
∴-
=f(log
4)=f(-2)=-f(2),
∴f(2)=
.
∵当x>0时,f(x)=ax(a>0,a≠1),
∴a2=
,解得a=
.
故选:D.
∴-
| 9 |
| 4 |
| 1 |
| 2 |
∴f(2)=
| 9 |
| 4 |
∵当x>0时,f(x)=ax(a>0,a≠1),
∴a2=
| 9 |
| 4 |
| 3 |
| 2 |
故选:D.
点评:本题考查了函数奇偶性、对数的运算性质,属于基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
若a=40.9,b=80.48,c=(
)-1.5.a,b,c的大小是( )
| 1 |
| 2 |
| A、a>b>c |
| B、a<b<c |
| C、a<c<b |
| D、b<c<a |
长方体ABCD-A1B1C1D1中,AB=3,BC=3,AA1=4,则二面角D1-AB-D的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
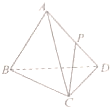 如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.
如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.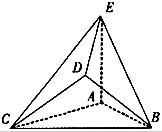 在如图所示的几何体中,是边长为2的正三角形,AE>1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
在如图所示的几何体中,是边长为2的正三角形,AE>1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.