题目内容
18．若复数z 满足z（1+i）=-2i（i为虚数单位），$\overline z$是z 的共轭复数，则$\overline z$•z=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 1 |
分析 把已知等式变形，利用复数代数形式的乘除运算化简，再由公式$z•\overline{z}=|z{|}^{2}$计算．
解答 解：由z（1+i）=-2i，得$z=\frac{-2i}{1+i}=\frac{-2i（1-i）}{（1+i）（1-i）}=-1-i$，
∴$\overline z$•z=|z|2=2．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．据统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系．对某小组学生每周用于数学学习时间x与数学成绩y进行数据收集如表：
由表中样本数据求回归直线方程$\stackrel{∧}{y}$=bx+a，则点（a，b）与直线x+18y=110的位置关系为是（ ）
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
| A． | 点在直线左侧 | B． | .点在直线右侧 | C． | .点在直线上 | D． | 无法确定 |
6．设集合A={x|x-3＜0}，B={y|y=2x，x∈[1，2]}，则A∩B=（ ）
| A． | ∅ | B． | （1，3） | C． | [2，3） | D． | （1，4] |
10．下方茎叶图如图1，为高三某班50名学生的数学考试成绩，算法框图如图2中输入的ai为茎叶图中的学生成绩，则输出的m，n分别是（ ）
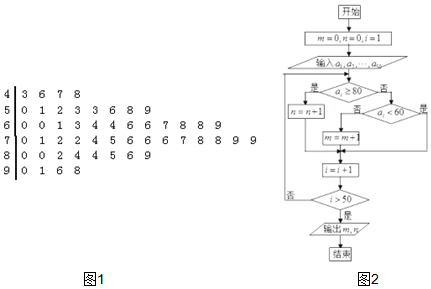
| A． | m=26，n=12 | B． | m=38，n=12 | C． | m=12，n=12 | D． | m=24，n=10 |
7．已知函数f（x）=$\left\{\begin{array}{l}{f（x-5）\\;x＞2}\\{a{e}^{x}\\;x≤2}\end{array}\right.$，若f（2017）=e2，则a=（ ）
| A． | 2 | B． | 1 | C． | -1 | D． | -2 |
8．
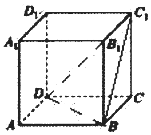在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）
在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |