题目内容
3.(a+$\frac{1}{x}$)(1-x)4的展开式中含x项的系数为-6,则常数a=3.分析 :(a+$\frac{1}{x}$)(1-x)4=$(a+\frac{1}{x})$(1-4x+${∁}_{4}^{2}$x2+…),则展开式中含x项的系数为-4a+6,即可得出.
解答 解:(a+$\frac{1}{x}$)(1-x)4=$(a+\frac{1}{x})$(1-4x+${∁}_{4}^{2}$x2+…),
则展开式中含x项的系数为-4a+6=-6,
解得a=3.
故答案为:3.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
13.已知数列{an}是等差数列,其前n项和为Sn,若a2a3a4=21,且$\frac{15}{{{S_3}{S_5}}}+\frac{35}{{{S_5}{S_7}}}+\frac{21}{{{S_7}{S_3}}}=\frac{3}{7}$.则a3等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
14.按照图中的程序框图执行,若M处条件是k>16,则输出结果为( )
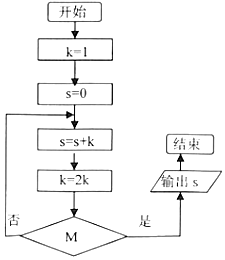

| A. | 15 | B. | 16 | C. | 31 | D. | 32 |
11.函数y=$\frac{1}{x}$+$\frac{1}{3-x}$(0<x<3)的最小值为( )
| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
18.若复数z 满足z(1+i)=-2i(i为虚数单位),$\overline z$是z 的共轭复数,则$\overline z$•z=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
8.在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,上顶点为B,M 为线段BF 的中点,若∠MOF=30°,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{1}{3}$ |
12.已知抛物线C:y2=4x的焦点为F,准线为l,过点F的直线交抛物线于A,B两点(A在第一象限),过点A作准线l的垂线,垂足为E,若∠AFE=60°,则△AFE的面积为( )
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
13.在等差数列{an}中,a2=3,a5+a7=10,则a1+a10=( )
| A. | 9 | B. | 9.5 | C. | 10 | D. | 11 |