题目内容

5．函数y=ax2+bx+3在（-∞，-1]上是增函数，在[-1，+∞）上是减函数，则（　　）
A．b＞0且a＜0B．b=2a＜0C．b=2a＞0D．b=-2a＜0

分析 若函数y=ax2+bx+3在（-∞，-1]上是增函数，在[-1，+∞）上是减函数，则a＜0，$-\frac{b}{2a}$=-1，进而得到答案．

解答 解：∵函数y=ax2+bx+3在（-∞，-1]上是增函数，在[-1，+∞）上是减函数，
∴a＜0，$-\frac{b}{2a}$=-1，
∴b=2a＜0，
故选：B

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
15．若${（{X-2}）^5}={a_5}{X^5}+{a_4}{X^4}+{a_3}{X^3}+{a_2}{X^2}+{a_1}X+{a_0}$，则a1+a2+a3+a4+a5=（　　）
A．-1B．31C．-33D．-31
16．三个数a=（-0.3）0，b=0.32，c=20.3的大小关系为（　　）
A．a＜b＜0B．a＜c＜bC．b＜c＜aD．b＜a＜c
13．设等比数列{an}的公比q=1，前n项和为Sn，则$\frac{{S}_{4}}{{a}_{2}}$=（　　）
A．2B．4C．$\frac{15}{2}$D．$\frac{17}{2}$
20．已知数列{an}中，${a_1}=\frac{3}{4}$，${a_n}=1-\frac{1}{{{a_{n-1}}}}$（n≥2），则a2016=（　　）
A．$\frac{3}{4}$B．$-\frac{1}{3}$C．$-\frac{3}{4}$D．4
10．若函数f（x）是定义在R上的偶函数，且图象经过点（-1，2），则f（-1）+f（1）=4．
17．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，长轴 A B上的100等分点从左到右依次为点 M1，M2，…，M99，过 Mi（i=1，2，…，99）点作斜率为k（k≠0）的直线li（i=1，2，…，99），依次交椭圆上半部分于点 P1，P3，P5，…，P197，交椭圆下半部分于点 P2，P4，P6，…，P198，则198条直线 A P1，A P2，…，A P198的斜率乘积为$-\frac{1}{{{2^{99}}}}$．
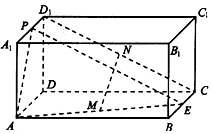14．如图，在长方体ABCD-A1B1C1D1中，E、P分别是BC、A1D1的中点．M、N分别是AE、CD1的中点，AD=AA1=$\frac{1}{2}$AB=2．
（1）求证：MN∥平面ADD1A1；
（2）求直线MN与平面PAE所成角的正弦值．
15．若集合A={-1，1}，B={0，1}，则集合A∪B的子集个数为（　　）
A．4B．5C．7D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网