Question

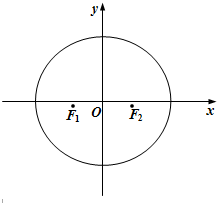如图所示，已知椭圆C的两个焦点分别为F₁（-1，0）、F₂（1，0），且F₂到直线x-

3

y-9=0的距离等于椭圆的短轴长．
（Ⅰ） 求椭圆C的方程；
（Ⅱ） 若圆P的圆心为P（0，t）（t＞0），且经过F₁、F₂，Q是椭圆C上的动点且在圆P外，过Q作圆P的切线，切点为M，当|QM|的最大值为

3 2

2

时，求t的值．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），利用条件求出b，c，a，得到椭圆C的方程．
（Ⅱ） 设Q（x，y）圆P的方程为x²+（y-t）²=t²+1，利用PM⊥QM，求出|OM|的表达式，通过-4t≤-2，当-4t＞-2，分别求解|QM|的最大值．求出t，推出结果．

解答： 解：（Ⅰ）设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），
依题意，2b=

|1-9|

2

=4，…（1分）
所以b=2…（2分）   又c=1，…（3分）
所以a²=b²+c²=5，…（4分）
所以椭圆C的方程为

x2

5

+

y2

4

=1．…（5分）
（Ⅱ） 设Q（x，y）（其中

x2

5

+

y2

4

=1），…（6分）
圆P的方程为x²+（y-t）²=t²+1，…（7分）
因为PM⊥QM，
所以|QM|=

|PQ|2-t2-1

=

x2+(y-t)2-t2-1

=

- 1 4 (y+4t)2+4+4t2

…（9分）
当-4t≤-2即t≥

1

2

时，当y=-2时，|QM|取得最大值，…（10分）
且|QM|max=

4t+3

=

3 2

2

，解得t=

3

8

＜

1

2

（舍去）．…（11分）
当-4t＞-2即0＜t＜

1

2

时，当y=-4t时，|QM|取最大值，…（12分）
且|QM|max=

4+4t2

=

3 2

2

，解得t2=

1

8

，又0＜t＜

1

2

，
所以t=

2

4

．…（13分）
综上，当t=

2

4

时，|QM|的最大值为

3 2

2

．…（14分）

点评：本题考查椭圆的标准方程的求法，直线与椭圆以及圆的位置关系，考查分析问题解决问题的能力．