题目内容
设曲线y=eax+sine在点(0,1)处的切线与直线x+2y+1=0垂直,则a= .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再根据两直线垂直建立等式关系,解之即可.
解答:
解:∵y=eax+sine,
∴y′=aeax
∴曲线y=eax在点(0,1)处的切线方程是y-1=a(x-0),即ax-y+1=0
∵直线ax-y+1=0与直线x+2y+1=0垂直
∴-
a=-1,即a=2.
故答案为:2.
∴y′=aeax
∴曲线y=eax在点(0,1)处的切线方程是y-1=a(x-0),即ax-y+1=0
∵直线ax-y+1=0与直线x+2y+1=0垂直
∴-
| 1 |
| 2 |
故答案为:2.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及两直线垂直的应用等有关问题,属于基础题.

练习册系列答案
相关题目
在等比数列{an}中,an>an+1,其前n项的积为Tn(n∈NΦ),若T13=4T9,则a8-a15=( )
| A、±2 | B、±4 | C、2 | D、4 |
下列命题:
①如果两条不重合的直线斜率相等,则它们平行;
②如果两直线平行,则它们的斜率相等;
③如果两直线的斜率之积为-1,则它们垂直;
④如果两直线垂直,则它们的斜率之积为-1.
其中正确的为( )
①如果两条不重合的直线斜率相等,则它们平行;
②如果两直线平行,则它们的斜率相等;
③如果两直线的斜率之积为-1,则它们垂直;
④如果两直线垂直,则它们的斜率之积为-1.
其中正确的为( )
| A、①②③④ | B、①③ |
| C、②④ | D、以上全错 |
下列命题是真命题的是( )
| A、a,b是两条直线,α是一个平面,b?α,若a∥b,则a∥α |
| B、若l∥α,则l平行与α内的所有直线 |
| C、m?α,l?β且l⊥m,则α⊥β |
| D、若l?β,l⊥α,则α⊥β |
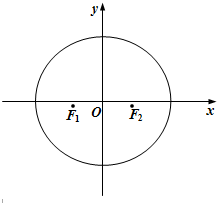 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x- 近年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标.PM2.5指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级:在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.淮北相山区2014年12月1日至I0日每天的PM2.5监测数据如茎叶图所示.
近年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标.PM2.5指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级:在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.淮北相山区2014年12月1日至I0日每天的PM2.5监测数据如茎叶图所示.