题目内容
在△ABC中,若AB=
,AC=1,∠C=
,则BC= .
| 7 |
| π |
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:先设BC=x,根据余弦定理列出方程,再把数据代入化简后求出BC的值.
解答:
解:设BC=x(x>0),
由余弦定理得,AB2=AC2+BC2-2AC•BCcos∠C,
因为AB=
,AC=1,∠C=
,
所以7=1+x2-2×1×x×cos
,化简得x2-x-6=0,
解得x=3或x=-2(舍去),即BC=3,
故答案为:3.
由余弦定理得,AB2=AC2+BC2-2AC•BCcos∠C,
因为AB=
| 7 |
| π |
| 3 |
所以7=1+x2-2×1×x×cos
| π |
| 3 |
解得x=3或x=-2(舍去),即BC=3,
故答案为:3.
点评:本题考查正弦、余弦定理的应用,此题若用正弦定理计算麻烦,选择余弦定理是解题的关键.

练习册系列答案
相关题目
设集合A={x|-1<x<3},集合B={x|x≥1},则A∩B=( )
| A、{x|1<x<3} |
| B、{x|1≤x<3} |
| C、{x|1<x≤3} |
| D、{x|1≤x≤3} |
已知
=(1,2),
=(-2,1),则
与
( )
| a |
| b |
| a |
| b |
| A、垂直 | B、不垂直也不平行 |
| C、平行且反向 | D、平行且同向 |
已知双曲线
-
=1的左右焦点分别为F1,F2,过左焦点F1作直线l与双曲线左右两支分别交于A、B两点,若△ABF2为正三角形,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、x±
| ||
B、x±
| ||
C、
| ||
D、
|
下列函数中,图象的一部分如图所示的是( )


A、y=sin(x+
| ||
B、y=sin(2x-
| ||
C、y=cos(4x-
| ||
D、y=cos(2x-
|
下列命题是真命题的是( )
| A、a,b是两条直线,α是一个平面,b?α,若a∥b,则a∥α |
| B、若l∥α,则l平行与α内的所有直线 |
| C、m?α,l?β且l⊥m,则α⊥β |
| D、若l?β,l⊥α,则α⊥β |
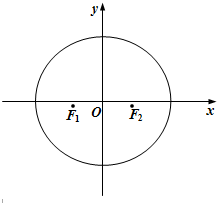 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-