题目内容
已知向量
=(1,3),
=(-3,4),则
在
方向上的投影为 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的含义与物理意义
专题:平面向量及应用
分析:根据向量投影的定义,计算
在
方向上的投影即可.
| a |
| b |
解答:
解:∵向量
=(1,3),
=(-3,4),
∴
在
方向上的投影为
|
|cos<
,
>=|
|×
=
=
=
.
故答案为:
.
| a |
| b |
∴
| a |
| b |
|
| a |
| a |
| b |
| a |
| ||||
|
|
=
| ||||
|
|
=
| 1×(-3)+3×4 | ||
|
=
| 9 |
| 5 |
故答案为:
| 9 |
| 5 |
点评:本题考查了平面向量投影的定义与应用问题,是基础题目.

练习册系列答案
相关题目
若双曲线
-
=1上一点P到它的右焦点距离是9,那么点P到它的左焦点的距离是( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、17 | ||
| B、17或1 | ||
C、4
| ||
| D、以上都错 |
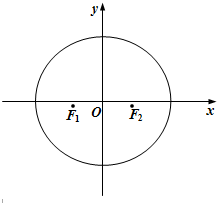 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-