题目内容
9. 一个几何体的三视图如图所示,设该几何体外接球为O,则过球O的一条半径中点且与半径垂直的圆的截面面积为( )
一个几何体的三视图如图所示,设该几何体外接球为O,则过球O的一条半径中点且与半径垂直的圆的截面面积为( )| A. | $\frac{9}{4}$π | B. | $\frac{9}{16}$π | C. | $\frac{27}{16}$π | D. | $\frac{27}{32}$π |
分析 由三视图判断出几何体是直四棱锥,且底面是长方形,再由外接球的结构特征,求出它的半径,代入表面积公式进行求解.
解答  解:由三视图判断出几何体是直四棱锥,其直观图如图所示,
解:由三视图判断出几何体是直四棱锥,其直观图如图所示,
外接球的直径是长、宽、高分别为2,1,2的长方体的对角线,长度为3,所以球的半径为$\frac{3}{2}$,
所以过球O的一条半径中点且与半径垂直的圆的截面圆半径为$\sqrt{(\frac{3}{2})^{2}-(\frac{3}{4})^{2}}$=$\sqrt{\frac{27}{16}}$,所以面积为$\frac{27}{16}π$;
故选C.
点评 本题考查了由三视图求几何体的体积,关键是对几何体正确还原,并根据三视图的长度求出几何体的几何元素的长度,还需要求出外接球的半径.考查了空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在等比数列{an}中,已知a1=1,a3=2a2,则该数列前6项和S6=( )
| A. | 31 | B. | 63 | C. | 127 | D. | 176 |
18.命题“若x=1,则x2-1=0”的否命题是( )
| A. | 若x=1,则x2-1≠0 | B. | 若x≠1,则x2-1=0 | C. | 若x≠1,则x2-1≠0 | D. | 若x2-1≠0,则x≠1 |

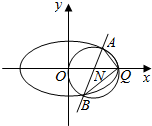 如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.
如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.