题目内容
已知ABCD是正方形,V是平面ABCD外一点,且VA=VB=VC=AB,求二面角A-VB-C的所成角的余弦值.
考点:二面角的平面角及求法
专题:空间角
分析:如图所示,建立空间直角坐标系.点O为正方形ABCD的对角线的交点,由于VA=VB=VC,可得VO⊥平面ABCD.
不妨取OA=1,可得A(0,-1,0),B(1,0,0),C(0,1,0),V(0,0,1).
=(1,0,-1),
=(1,1,0),
=(-1,1,0).分别求出平面VAB与平面VBC的法向量,利用法向量的夹角即可得出二面角的平面角的余弦值.
不妨取OA=1,可得A(0,-1,0),B(1,0,0),C(0,1,0),V(0,0,1).
| VB |
| AB |
| BC |
解答:
解:如图所示, 建立空间直角坐标系.
建立空间直角坐标系.
点O为正方形ABCD的对角线的交点,
∵VA=VB=VC,
∴VO⊥平面ABCD.
不妨取OA=1,
则A(0,-1,0),B(1,0,0),C(0,1,0),V(0,0,1).
=(1,0,-1),
=(1,1,0),
=(-1,1,0).
设平面VAB的法向量为
=(x,y,z),
则
,
取
=(1,-1,1).
同理可得:平面VBC的法向量
=(1,1,1).
∴cos<
,
>=
=
=
.
由图形可知:二面角A-VB-C的所成角为钝角,
∴二面角A-VB-C的所成角的余弦值为-
.
 建立空间直角坐标系.
建立空间直角坐标系.点O为正方形ABCD的对角线的交点,
∵VA=VB=VC,
∴VO⊥平面ABCD.
不妨取OA=1,
则A(0,-1,0),B(1,0,0),C(0,1,0),V(0,0,1).
| VB |
| AB |
| BC |
设平面VAB的法向量为
| n |
则
|
取
| n |
同理可得:平面VBC的法向量
| m |
∴cos<
| m |
| n |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 3 |
由图形可知:二面角A-VB-C的所成角为钝角,
∴二面角A-VB-C的所成角的余弦值为-
| 1 |
| 3 |
点评:本题考查了通过建立空间直角坐标系利用两个平面的法向量的夹角可得出二面角的平面角的余弦值的方法,考查了空间想象能力.考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
函数y=10|x+1|-1的单调减区间为( )
| A、(-∞,-1) |
| B、(-∞,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
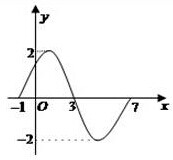 如图为函数y1=Asin(ωx+φ)(|φ|<
如图为函数y1=Asin(ωx+φ)(|φ|<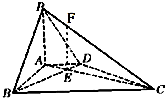 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC和BD交于点E,PA=3,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC和BD交于点E,PA=3,AD=2,AB=2