题目内容
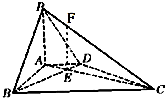如图，在底面为直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，AC和BD交于点E，PA=3，AD=2，AB=2| 3 |
（1）若在PC取一点F，满足
| PF |
| FC |
| 1 |
| 3 |
（2）求证：BD⊥平面PAC．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由AD∥BC，可得
=
=
，而
=
，可得
=
．因此EF∥PA．再利用线面平行的判定定理即可得出．
（2）由PA⊥平面ABCD，可得PA⊥BD．在直角梯形ABCD中，过点D作DM∥AC交BC的延长线于点M．由AD∥BC，∠ABC=90°，AD=2，AB=2
，BC=6．可得BD2+DM2=BM2，因此BD⊥DM．利用线面垂直的判定定理即可得出．
| AE |
| EC |
| AD |
| BC |
| 1 |
| 3 |
| PF |
| FC |
| 1 |
| 3 |
| AE |
| EC |
| PF |
| FC |
（2）由PA⊥平面ABCD，可得PA⊥BD．在直角梯形ABCD中，过点D作DM∥AC交BC的延长线于点M．由AD∥BC，∠ABC=90°，AD=2，AB=2
| 3 |
解答：
证明：（1）∵AD∥BC，∴
=
=
，
∵
=
，
∴
=
．
∴EF∥PA．
∵EF?平面PAB，PA?平面PAB．
∴EF∥平面PAB；
（2）∵PA⊥平面ABCD，
∴PA⊥BD．
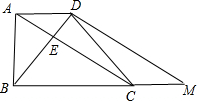
在直角梯形ABCD中，过点D作DM∥AC交BC的延长线于点M．
∵AD∥BC，∠ABC=90°，AD=2，AB=2
，BC=6．
∴BD=
=4，AC=
=4
．
∴BD2+DM2=BM2=82，
∴BD⊥DM．
即BD⊥AC．
又AC∩PA=A，
∴BD⊥平面PAC．
证明：（1）∵AD∥BC，∴| AE |
| EC |
| AD |
| BC |
| 1 |
| 3 |
∵
| PF |
| FC |
| 1 |
| 3 |
∴
| AE |
| EC |
| PF |
| FC |
∴EF∥PA．
∵EF?平面PAB，PA?平面PAB．
∴EF∥平面PAB；
（2）∵PA⊥平面ABCD，
∴PA⊥BD．
在直角梯形ABCD中，过点D作DM∥AC交BC的延长线于点M．
∵AD∥BC，∠ABC=90°，AD=2，AB=2
| 3 |
∴BD=
| AB2+AD2 |
| AB2+BC2 |
| 3 |
∴BD2+DM2=BM2=82，
∴BD⊥DM．
即BD⊥AC．
又AC∩PA=A，
∴BD⊥平面PAC．
点评：本题考查了线面平行与垂直的判定定理、勾股定理、平行线分线段成比例定理、梯形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知i是虚数单位，z1=2014+2014i，z2=1-3i，则z=
在复平面内对应的点在（ ）
| ||
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |