题目内容
4.若函数f(x)=x+$\frac{(2a-1)x+1}{x}$为奇函数,则a=$\frac{1}{2}$.分析 根据函数奇偶性的性质建立方程关系进行求解即可.
解答 解:f(x)=x+$\frac{(2a-1)x+1}{x}$=x+(2a-1)+$\frac{1}{x}$,函数的定义域为{x|x≠0},
∵f(x)是奇函数,
∴f(-x)=-f(x),
则-x+(2a-1)-$\frac{1}{x}$=-(x+(2a-1)+$\frac{1}{x}$)=-x-(2a-1)-$\frac{1}{x}$,
即2a-1=-(2a-1),
则2a-1=0,得a=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题主要考查函数奇偶性的应用,根据奇函数的性质建立方程关系是解决本题的关键.

练习册系列答案
相关题目
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1,F2,两条渐近线分别为l1,l2,过F1作F1A⊥l1于点A,过F2作F2B⊥l2于点B,O为原点,若△ABO是边长为$\sqrt{3}$的等边三角形,则双曲线的方程为( )
| A. | $\frac{x^2}{21}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{21}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{3}=1$ |
19.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…,则此数列第20项为( )
| A. | 180 | B. | 200 | C. | 128 | D. | 162 |
16.下列命题正确的是( )
(1)若命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
(2)命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;
(3)“x=4”是“x2-3x-4=0”的必要不充分条件;
(4)命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
(1)若命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
(2)命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;
(3)“x=4”是“x2-3x-4=0”的必要不充分条件;
(4)命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
| A. | (2)(3) | B. | (1)(2)(3) | C. | (2)(4) | D. | (2)(3)(4) |
13.函数y=tan $\frac{x}{2}$是( )
| A. | 周期为2π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
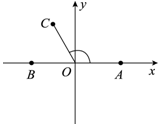 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.