题目内容
某汽车4s店统计了2至5月期间,该店销售的汽车y(单位:辆) 与月份x(单位:月)的关系数据如下表:
根据上表,得到回归直线方程
=10x+a,已知该店在6月搞促销活动,由回归直线方程预报汽车的销售量是67,则m+n= .
| 月份x | 2 | 3 | 4 | 5 |
| 销售量y | 26 | m | n | 54 |
 |
| y |
考点:线性回归方程
专题:计算题,概率与统计
分析:将(6,67)代入y=10x+a,可得a;求出样本中心点,代入y=10x+a,可得m+n的值.
解答:
解:由题意,将(6,67)代入y=10x+a,可得a=7
=
(2+3+4+5)=3.5,
=
(80+m+n),
代入y=10x+a,可得
(80+m+n)=35+a,
∴m+n=88.
故答案为:88.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
代入y=10x+a,可得
| 1 |
| 4 |
∴m+n=88.
故答案为:88.
点评:本题考查回归直线方程的求法,是统计中的一个重要知识点,由公式得到样本中心点在回归直线上是关键.

练习册系列答案
相关题目
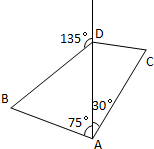 如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距
如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距