题目内容
10．在△ABC中，a2+b2＞c2，$sinC=\frac{{\sqrt{3}}}{2}$，则∠C的大小为$\frac{π}{3}$．分析 直接利用勾股定理，判断三角形的形状，通过sinC=$\frac{\sqrt{3}}{2}$，求出∠C的值．
解答 解：因为在△ABC中，若a2+b2＞c2，
所以∠C＜$\frac{π}{2}$，又sinC=$\frac{\sqrt{3}}{2}$，
所以∠C=$\frac{π}{3}$．
故答案为：$\frac{π}{3}$．
点评 本题是基础题，考查三角形的有关计算，勾股定理、余弦定理的应用，考查计算能力．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
18．命题“若x=1，则x2-1=0”的否命题是（ ）
| A． | 若x=1，则x2-1≠0 | B． | 若x≠1，则x2-1=0 | C． | 若x≠1，则x2-1≠0 | D． | 若x2-1≠0，则x≠1 |
2．下列各式中，正确的是（ ）
| A． | sin（-$\frac{π}{8}$）＞sin（-$\frac{π}{10}$） | B． | cos（-$\frac{23π}{5}$）＞cos（-$\frac{17π}{4}$） | ||
| C． | cos250°＞cos260° | D． | tan144°＜tan148° |
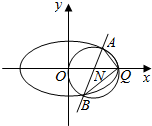如图，已知焦点在x轴上的椭圆C过点（-2，0），且离心率为$\frac{\sqrt{3}}{2}$，Q为椭圆C的右顶点．