题目内容
某学校要建造一个面积为10 000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
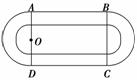
(1)设半圆的半径OA=r(米),设建立塑胶跑道面积S与r的函数关系S(r);
(2)由于条件限制r∈[30,40],问当r取何值时,运动场造价最低?最低造价为多少?(精确到元)
解析 (1)塑胶跑道面积
S=π[r2-(r-8)2]+8× ×2
×2
= +8πr-64π.
+8πr-64π.
∵πr2<10 000,∴0<r< .
.
(2)设运动场的造价为y元,
y=150×
+30×
=300 000+120× -7 680π.
-7 680π.
令f(r)= +8πr,
+8πr,
∵f′(r)=8π- ,
,
当r∈[30,40]时,f′(r)<0,
∴函数y=300 000+120× -7 680π
-7 680π
在[30,40]上为减函数.
∴当r=40时,ymin≈636 510,
即运动场的造价最低为636 510元.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

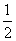 x2+2x+20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
x2+2x+20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )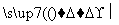 密文
密文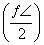 +f2
+f2