题目内容
设函数f(x)=ax2+bx+c(a≠0)满足f(x+1)=f(-x-3),且f(-2)>f(2),解不等式:f(-2x2+2x-3)>f(x2+4x+3)
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出函数的对称轴,得到函数的单调性,问题转化为|-2x2+2x-3-(-1)|<|x2+4x+3-(-1)|,即|2x2-2x+2|<|x2+4x+4|,解出即可.
解答:
解:二次函数f(x)=ax2+bx+c满足:
f(x+1)=f(-x-3)
则对称轴x=
=-1,
∴f(0)=f(-2)
∵f(-2)>f(2)⇒f(0)>f(2)
∴f(x)在区间[-1,+∞)上为减函数
f(-2x2+2x-3)>f(x2+4x+3)⇒
|-2x2+2x-3-(-1)|<|x2+4x+3-(-1)|
所以:|2x2-2x+2|<|x2+4x+4|
∵两个绝对值内的数恒为非负数
∴2x2-2x+2<x2+4x+4
⇒x2-6x-2<0
⇒3-
<x<3+
.
f(x+1)=f(-x-3)
则对称轴x=
| (x+1)+(-x-3) |
| 2 |
∴f(0)=f(-2)
∵f(-2)>f(2)⇒f(0)>f(2)
∴f(x)在区间[-1,+∞)上为减函数
f(-2x2+2x-3)>f(x2+4x+3)⇒
|-2x2+2x-3-(-1)|<|x2+4x+3-(-1)|
所以:|2x2-2x+2|<|x2+4x+4|
∵两个绝对值内的数恒为非负数
∴2x2-2x+2<x2+4x+4
⇒x2-6x-2<0
⇒3-
| 11 |
| 11 |
点评:本题考查了二次函数的性质,考查了函数的单调性,考查了不等式问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=2sin(ωx+ϕ)(ω>0,-
<ϕ<
)的部分图象如图所示,则ω,φ的值分别是( )

| π |
| 2 |
| π |
| 2 |

A、2,-
| ||||
B、2,-
| ||||
C、
| ||||
D、
|
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1则该三棱柱的体积为
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1则该三棱柱的体积为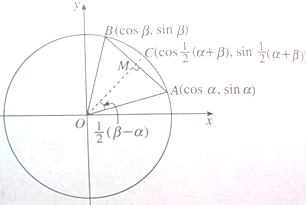 你能利用如图,给出下列两个等式的一个证明吗?
你能利用如图,给出下列两个等式的一个证明吗?