题目内容
20.在△ABC中,∠C=90°,且CA=CB=3,点M满足$\overrightarrow{BM}$=3$\overrightarrow{AM}$,则$\overrightarrow{CM}$•$\overrightarrow{CA}$=$\frac{27}{2}$.分析 由题意画出图形,把$\overrightarrow{CM}$用$\overrightarrow{CA}、\overrightarrow{CB}$表示,代入$\overrightarrow{CM}$•$\overrightarrow{CA}$得答案.
解答 解:如图,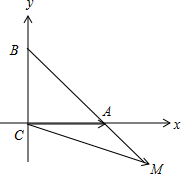
∵$\overrightarrow{BM}$=3$\overrightarrow{AM}$,CA=CB=3,
∴$\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}=\overrightarrow{CA}+\frac{1}{2}\overrightarrow{BA}$=$\overrightarrow{CA}+\frac{1}{2}(\overrightarrow{CA}-\overrightarrow{CB})=\frac{3}{2}\overrightarrow{CA}-\frac{1}{2}\overrightarrow{CB}$.
∴$\overrightarrow{CM}$•$\overrightarrow{CA}$=$(\frac{3}{2}\overrightarrow{CA}-\frac{1}{2}\overrightarrow{CB})•\overrightarrow{CA}=\frac{3}{2}|\overrightarrow{CA}{|}^{2}=\frac{27}{2}$.
故答案为:$\frac{27}{2}$.
点评 本题考查平面向量的数量积运算,考查共线向量基本定理及向量加减法法则的应用,是中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
12.设φ∈R,则“φ=0”是“f(x)=cos(2x+φ)(x∈R)为偶函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
9.若集合$M=\{x\left|{\frac{1}{x}<1}\right.\}$,集合S={x|y=lg(x-1)},则下列各式中正确的是( )
| A. | M∪S=M | B. | M∪S=S | C. | M=S | D. | M∩S=∅ |
 为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示,已知样本中体重在区间(45,50]上的女生数与体重在区间(50,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示,已知样本中体重在区间(45,50]上的女生数与体重在区间(50,60]上的女生数之比为4:3.