题目内容
20.设f(x)是定义在R上的奇函数,且f(2-x)=f(x),当-1≤x<0时,f(x)=log2(-3x+1),则f(2017)的值为( )| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
分析 根据题意,由函数的奇偶性以及f(2-x)=f(x)分析可得f(2+x)=-f(x),进而可得f(4+x)=f(x),则函数f(x)的周期为4;则f(2017)=f(5×504+1)=f(1)=-f(-1),由-1≤x<0时,函数的解析式计算可得答案.
解答 解:根据题意,f(x)是定义在R上的奇函数,且f(2-x)=f(x),
则有f(2+x)=-f(x),
则f(4+x)=f[2+(2+x)]=-f(2+x)=f(x),则函数f(x)的周期为4,
f(2017)=f(5×504+1)=f(1)=-f(-1)=-log2[(-3)×(-1)+1]=-2,
即f(2017)=-2;
故选:B.
点评 本题考查函数的奇偶性、周期性的应用,关键是求出该函数的周期.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.为了得到函数$y={log_2}\frac{x+1}{4}$的图象,只需把函数y=log2x的图象上所有的点( )
| A. | 向左平移1个单位长度,再向上平移2个单位长度 | |
| B. | 向右平移1个单位长度,再向上平移2个单位长度 | |
| C. | 向左平移1个单位长度,再向下平移2个单位长度 | |
| D. | 向右平移1个单位长度,再向下平移2个单位长度 |
12.已知椭圆E的离心率为e,两焦点分别为F1,F2,抛物线C以F1为顶点,F2为焦点,点P为这两条曲线的一个交点,若e|$\overrightarrow{P{F_2}}$|=|$\overrightarrow{P{F_1}}$|,则e的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 不能确定 |
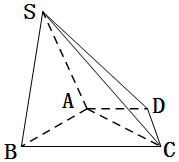 如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.
如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.