题目内容
15.已知F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线PP′过坐标原点O,与椭圆C分别交于点P,P′两点,且|PF|=1,|P′F|=3,椭圆C的离心率e=$\frac{1}{2}$(Ⅰ)求椭圆C的方程;
(Ⅱ)直线l过椭圆C的右焦点F,且与椭圆C交于A,B两点,若∠AOB是钝角,求直线l的斜率k的取值范围.
分析 (Ⅰ)由题意可知丨PF1丨+|PF|=3+1=4=2a,a=2c,即可求得c的值,b2=a2-c2=3,即可求得椭圆C的方程;
(Ⅱ)当k=0时,求得A和B的坐标,由$\overrightarrow{OA}$•$\overrightarrow{OB}$=1-$\frac{3}{4}$=$\frac{1}{4}$>0,则∠AOB是锐角,当k≠0,代入椭圆方程,由韦达定理及向量的坐标运算,x1x2+y1y2<0,即可求得k的取值范围.
解答 解:(Ⅰ)设椭圆的左焦点为F1,由题意可在:丨PF1丨=|P′F|=3,则丨PF1丨+|PF|=3+1=4=2a,则a=2,
椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则c=1,
b2=a2-c2=3
椭圆C的方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)由(Ⅱ)可知:椭圆的右焦点(1,0),直线AB的斜率k=0时,
A(1,$\frac{\sqrt{3}}{2}$),A(1,-$\frac{\sqrt{3}}{2}$),
$\overrightarrow{OA}$•$\overrightarrow{OB}$=1-$\frac{3}{4}$=$\frac{1}{4}$>0,
∴∠AOB是锐角,
当直线AB的斜率存在时,直线l的方程y=k(x-1),k≠0,A(x1,y1),B(x2,y2).
则$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得(3+4k2)x2-8k2x+4k2-12=0,
∵直线l过焦点F,∴△>0恒成立,
且x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
∠AOB是钝角,则$\overrightarrow{OA}$•$\overrightarrow{OB}$<0,
∴x1x2+y1y2<0,x1x2+k2(x1-1)(x2-1)<0,化为:(1+k2)x1x2-k2(x1+x2)+k2<0,
则(1+k2)×$\frac{4{k}^{2}-12}{3+4{k}^{2}}$-k2×$\frac{8{k}^{2}}{3+4{k}^{2}}$+k2<0,解得:k2≥-$\frac{12}{5}$,
综上可知:k∈R,且k≠0,
直线l的斜率k的取值范围(-∞,0)∪(0,+∞).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案| A. | 为定值8 | B. | 为定值4 | C. | 为定值2 | D. | 不是定值 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 3 | B. | 3i | C. | -3 | D. | -3i |
| A. | (-∞,-2]∪[2,+∞) | B. | [0,2] | C. | $[-\sqrt{2},\sqrt{2}]$ | D. | [-2,2] |
(1)请将列联表补充完整;
| 患三高疾病 | 不患三高疾病 | 合计 | |
| 男 | 24 | 6 | 30 |
| 女 | 12 | 18 | 30 |
| 合计 | 36 | 24 | 60 |
下列的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
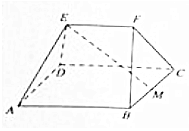 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.