题目内容
10.已知函数f(x)=$\frac{a}{x}$+x+lnx,a∈R.(1)设曲线y=f(x)在x=1处的切线与直线x+2y-1=0平行,求此切线方程;
(2)当a=0时,令函数g(x)=f(x)-$\frac{1}{2b}$x2-x(b∈R且b≠0),求函数g(x)在定义域内的极值点.
分析 (1)求导数,利用曲线y=f(x)在x=1处的切线与直线x+2y-1=0平行,求出a,可得切点坐标,即可求此切线方程;
(2)分类讨论,求导数,利用极值的定义,可得函数g(x)在定义域内的极值点.
解答 解:(1)由题意知:f′(x)=-$\frac{a}{{x}^{2}}$+1+$\frac{1}{x}$,
∴k=f′(1)=-a+2=-$\frac{1}{2}$,
∴a=$\frac{5}{2}$,切点为(1,$\frac{7}{2}$),
∴此切线方程为y-$\frac{7}{2}$=-$\frac{1}{2}$(x-1),
即x+2y-8=0.
(2)当a=0时,g(x)=x+lnx-$\frac{1}{2b}$x2-x=lnx-$\frac{1}{2b}$x2,定义域为x∈(0,+∞),
∴g′(x)=$\frac{1}{x}$-$\frac{x}{b}$=$\frac{b{-x}^{2}}{bx}$,
①当b<0时,∴g′(x)>0恒成立,
∴g(x)在x∈(0,+∞)上为增函数,
∴g(x)在定义域内无极值;
②当b>0时,令g′(x)=0,∴x=$\sqrt{b}$或x=-$\sqrt{b}$(舍去),
| x | (0,$\sqrt{b}$) | $\sqrt{b}$ | ($\sqrt{b}$,+∞) |
| g′(x) | + | 0 | - |
| g(x) | ↑ | 极大值 | ↓ |
综上:当b<0时,g(x)在定义域内无极值;
当b>0时,g(x)的极大值点为$\sqrt{b}$,无极小值点.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的极值,考查恒成立问题,考查学生分析解决问题的能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
1.已知实数x,y满足约束条件$\left\{{\begin{array}{l}{x+y+1≥0}\\{{x^2}+{y^2}≤4}\\{xy≥0}\end{array}}\right.$,则z=2x+y的取值范围是( )
| A. | $[-2,2\sqrt{5}]$ | B. | [-2,0] | C. | $[-2\sqrt{5},2]$ | D. | $[\frac{{2\sqrt{5}}}{5},1]$ |
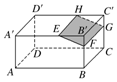 如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.
如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.