题目内容
11.为了得到函数$y={log_2}\frac{x+1}{4}$的图象,只需把函数y=log2x的图象上所有的点( )| A. | 向左平移1个单位长度,再向上平移2个单位长度 | |
| B. | 向右平移1个单位长度,再向上平移2个单位长度 | |
| C. | 向左平移1个单位长度,再向下平移2个单位长度 | |
| D. | 向右平移1个单位长度,再向下平移2个单位长度 |
分析 利用对数的运算性质化简平移目标函数的解析式,然后根据“左加右减,上加下减”的原则,可得答案.
解答 解:∵函数$y={log_2}\frac{x+1}{4}$=log2(x+1)-log24=log2(x+1)-2,
故其图象可由函数y=log2x的图象向左平移1个单位长度,再向下平移2个长度单位得到,
故选C.
点评 本题以对数函数图象平移为载体,考查了对数的运算性质,其中利用对数的运算性化间平移目标函数的解析式,是解答的核心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知实数x,y满足约束条件$\left\{{\begin{array}{l}{x+y+1≥0}\\{{x^2}+{y^2}≤4}\\{xy≥0}\end{array}}\right.$,则z=2x+y的取值范围是( )
| A. | $[-2,2\sqrt{5}]$ | B. | [-2,0] | C. | $[-2\sqrt{5},2]$ | D. | $[\frac{{2\sqrt{5}}}{5},1]$ |
6.在复平面内,复数z=$\frac{1-\sqrt{2}i}{i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.复数$\frac{3+4i}{i}$的虚部为( )
| A. | 3 | B. | 3i | C. | -3 | D. | -3i |
1.底面为正方形且侧棱与底面垂直的四棱柱与圆锥的组合体的三视图,如图所示,则该组合体的体积为( )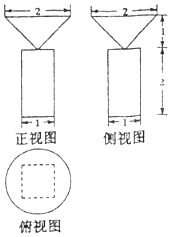

| A. | $\frac{π}{3}$+2 | B. | $\frac{π}{3}$+$\frac{2}{3}$ | C. | π$+\frac{2}{3}$ | D. | π+2 |