题目内容
12.已知椭圆E的离心率为e,两焦点分别为F1,F2,抛物线C以F1为顶点,F2为焦点,点P为这两条曲线的一个交点,若e|$\overrightarrow{P{F_2}}$|=|$\overrightarrow{P{F_1}}$|,则e的值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 不能确定 |
分析 利用椭圆的第二定义及e|$\overrightarrow{P{F_2}}$|=|$\overrightarrow{P{F_1}}$|,求得丨PT丨=丨PF2丨,则(-c)-(-$\frac{{a}^{2}}{c}$)=c-(-c),即可求得a与c的关系,即可求得e的值.
解答 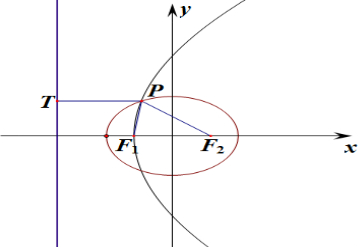 解:作PT垂直椭圆准线l于T,则由椭圆第二定义:丨PF1丨:丨PT丨=e
解:作PT垂直椭圆准线l于T,则由椭圆第二定义:丨PF1丨:丨PT丨=e
又$\frac{丨\overrightarrow{P{F}_{1}}丨}{丨\overrightarrow{P{F}_{2}}丨}$=e,
故丨PT丨=丨PF2丨,
由抛物线定义知l为抛物线准线
故F1到l的距离等于F1到F2的距离,
即(-c)-(-$\frac{{a}^{2}}{c}$)=c-(-c),整理得:a=$\sqrt{3}$c,
e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,
故选C.
点评 本题考查椭圆的简单几何性质,考查椭圆的第二定义,考查数形结合思想,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
3.复数$\frac{3+4i}{i}$的虚部为( )
| A. | 3 | B. | 3i | C. | -3 | D. | -3i |
7.食品添加剂会引起血脂增高、血压增高、血糖增高等疾病,为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
(2)为了研究三高疾病是否与性别有关,请计算出统计量K2,并说明你有多大把握认为患三高疾病与性别有关.
下列的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
(1)请将列联表补充完整;
| 患三高疾病 | 不患三高疾病 | 合计 | |
| 男 | 24 | 6 | 30 |
| 女 | 12 | 18 | 30 |
| 合计 | 36 | 24 | 60 |
下列的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.底面为正方形且侧棱与底面垂直的四棱柱与圆锥的组合体的三视图,如图所示,则该组合体的体积为( )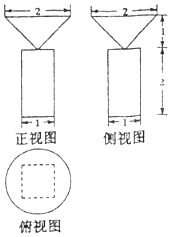

| A. | $\frac{π}{3}$+2 | B. | $\frac{π}{3}$+$\frac{2}{3}$ | C. | π$+\frac{2}{3}$ | D. | π+2 |
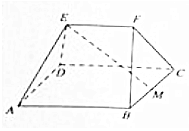 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.