题目内容

17．在等差数列{an}中an＞0，且a1+a2+…+a20=60，则a10•a11的最大值等于（　　）
A．3B．6C．9D．36

分析 由等差数列{an}的性质及其a1+a2+…+a20=60，可得$\frac{20（{a}_{1}+{a}_{20}）}{2}$=$\frac{20（{a}_{10}+{a}_{11}）}{2}$=60，再利用基本不等式的性质即可得出．

解答 解：由等差数列{an}的性质及其a1+a2+…+a20=60，
∴$\frac{20（{a}_{1}+{a}_{20}）}{2}$=$\frac{20（{a}_{10}+{a}_{11}）}{2}$=60，
∴a10+a11=6，又an＞0，
∴$6≥2\sqrt{{a}_{10}•{a}_{11}}$，
∴a10•a11≤9，
故选：C．

点评 本题考查了等差数列的通项公式及其性质与前n项和公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
3．如图，直线l经过第二、第三、第四象限，l的倾斜角为α，斜率为k，则（　　）
A．ksin（π+α）＞0B．kcos（π-α）＞0C．ksinα≤0D．kcosα≤0
8．中心在坐标原点O，焦点在坐标轴上的椭圆E经过两点$R（{-\frac{{\sqrt{3}}}{2}，-\frac{{\sqrt{6}}}{2}}），Q（{\frac{3}{2}，\frac{{\sqrt{2}}}{2}}）$．分别过椭圆E的焦点F1、F2的动直线l1，l2相交于P点，与椭圆E分别交于A、B与C、D不同四点，直线OA、OB、OC、OD的斜率k1、k2、k3、k4满足k1+k2=k3+k4．
（1）求椭圆E的方程；
（2）是否存在定点M、N，使得|PM|+|PN|为定值．若存在，求出M、N点坐标并求出此定值，若不存在，说明理由．
5．一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，则这个平面图形的面积为（　　）
A．$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$B．1+$\frac{\sqrt{2}}{2}$C．1+$\sqrt{2}$D．2+$\sqrt{2}$
12．在长方体ABCD-A1B1C1D1中，二面角D-AB-D1的大小为45°，DC1与平面ABCD所成角的大小为30°，那么异面直线AD1与DC1所成角的余弦值是（　　）
A．$\frac{{\sqrt{3}}}{4}$B．$\frac{{\sqrt{2}}}{4}$C．$\frac{{\sqrt{2}}}{8}$D．$\frac{{\sqrt{3}}}{8}$
2．已知函数f（x）=$\left\{\begin{array}{l}{|lgx|，0＜x≤3}\\{f（6-x），3＜x＜6}\end{array}\right.$，设方程f（x）=2-x+b（b∈R）的四个实根从小到大依次为x1，x2，x3，x4，对于满足条件的任意一组实根，下列判断中一定正确的为（　　）
A．x1+x2=2B．9＜x3•x4＜25C．0＜（6-x3）•（6-x4）＜1D．1＜x1•x2＜9
9．若集合U={1，2，3，4，5}，A={1，2，3}，B={2，3，4}，则∁U（A∪B）=（　　）
A．{5}B．{2}C．{1，2，3，4}D．{1，3，4，5}
6．如图，在正四棱柱ABCD-A1B1C1D1中，E，F分别是AB1，BC1的中点，则以下结论中不成立的是（　　）
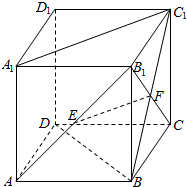
A．EF与BB1垂直B．EF与BD垂直C．EF与CD异面D．EF与A1C1异面
7．函数f（x）=x2-1（2＜x＜3）的反函数为（　　）
A．f-1（x）=$\sqrt{x-1}$（3＜x＜8）B．f-1（x）=$\sqrt{x+1}$（3＜x＜8）C．f-1（x）=$\sqrt{x-1}$（4＜x＜9）D．f-1（x）=$\sqrt{x+1}$（4＜x＜9）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网