题目内容
5.一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,则这个平面图形的面积为( )| A. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
分析 根据斜二测画法还原出原平面图形,求出它的面积即可.
解答  解:把直观图还原出原平面图形,如图所示;
解:把直观图还原出原平面图形,如图所示;
∴这个平面图形是直角梯形,
它的面积为
S=$\frac{1}{2}$×(1+1+$\sqrt{2}$)×2
=2+$\sqrt{2}$.
故选:D.
点评 本题考查了斜二测画法画直观图的应用问题,解题的关键是还原出原平面图形,是基础题.

练习册系列答案
相关题目
17.在等差数列{an}中an>0,且a1+a2+…+a20=60,则a10•a11的最大值等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
14.已知${2^x}>{(\frac{1}{2})^{x-1}}$,则x的取值范围是( )
| A. | R | B. | $x<\frac{1}{2}$ | C. | $x>\frac{1}{2}$ | D. | ∅ |
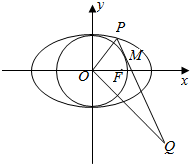 在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.
在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M. 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形ABCD的面积为32$\sqrt{3}$.
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形ABCD的面积为32$\sqrt{3}$.