题目内容
数列{an}满足a1=
,
=
-1(n∈N*),则a10=( )
| 1 |
| 2 |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:等差数列与等比数列
分析:两条等差数列的通项公式即可得出.
解答:
解:∵
=
-1(n∈N*),
∴
-
=-1,
∴数列{
}是等差数列,首项为
=-2,公差为-1.
∴
=-2-(n-1)=-n-1,
∴an=1-
=
.
∴a10=
.
故选:C.
| 1 |
| an+1-1 |
| 1 |
| an-1 |
∴
| 1 |
| an+1-1 |
| 1 |
| an-1 |
∴数列{
| 1 |
| an-1 |
| 1 |
| a1-1 |
∴
| 1 |
| an-1 |
∴an=1-
| 1 |
| n+1 |
| n |
| n+1 |
∴a10=
| 10 |
| 11 |
故选:C.
点评:本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
在平行四边形ABCD中,
=3
,AE的延长线与CD交于点F,若
=
,
=
,则
=( )
| BD |
| ED |
| AC |
| a |
| BD |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
设函数f(x)=|lnx|-
的两个零点为x1,x2,则有( )
| 1 |
| x+1 |
| A、x1x2<1 | ||
| B、x1x2=1 | ||
C、1<x1x2<
| ||
D、x1x2≥
|
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
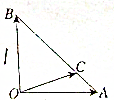 如图所示,在等腰Rt△AOB中,OA=OB=1,
如图所示,在等腰Rt△AOB中,OA=OB=1,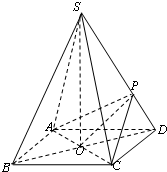 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的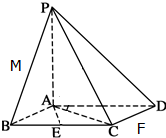 如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.
如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.