题目内容
18.已知函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
| A. | $\frac{1}{2}$,$\frac{π}{6}$ | B. | 1,$\frac{π}{6}$ | C. | 1,$\frac{π}{3}$ | D. | $\frac{1}{2}$,$\frac{π}{3}$ |
分析 由周期求出ω,由五点法作图求出φ的值,可得结论.
解答 解:由函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象知,$\frac{1}{4}•\frac{2π}{ω}$=$\frac{2π}{3}$+$\frac{π}{3}$=π,∴ω=$\frac{1}{2}$.
再根据五点法作图可得$\frac{1}{2}$•(-$\frac{π}{3}$)+φ=0,∴φ=$\frac{π}{6}$,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.设集合A={x|x2+3x-4>0},集合B={x|-2<x≤3},且M=A∩B,则有( )
| A. | 1∈M | B. | 0∈M | C. | 1∈M | D. | 2∈M |
6.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为( )
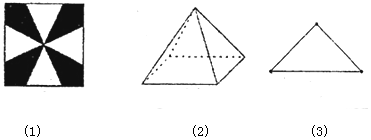

| A. | $12\sqrt{6}c{m^3}$ | B. | $4\sqrt{6}c{m^3}$ | C. | $27\sqrt{2}c{m^3}$ | D. | $9\sqrt{2}c{m^3}$ |
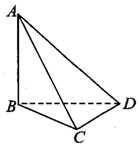
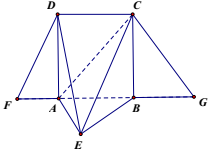 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.