��Ŀ����
13��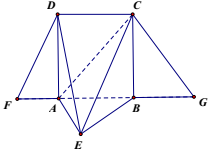 ��ͼ������FDCG��DC��FG������D��C��DA��FG��CB��FG������ֱ�ΪA��B����DA=AB=2���ֽ���DAF��DA����CBG��CB���ۣ�ʹ�õ�F��G�غϣ���ΪE���ҵ�B����AEC����Ӱ���߶�EC�ϣ�
��ͼ������FDCG��DC��FG������D��C��DA��FG��CB��FG������ֱ�ΪA��B����DA=AB=2���ֽ���DAF��DA����CBG��CB���ۣ�ʹ�õ�F��G�غϣ���ΪE���ҵ�B����AEC����Ӱ���߶�EC�ϣ�������֤��AE��EB��
������$\frac{AF}{BG}$=�ˣ��Ƿ���ڦˣ�ʹ�����B-AC-E������ֵΪ$\frac{\sqrt{3}}{3}$�������ڣ���˵�ֵ���������ڣ�˵�����ɣ�
���� ��������֪�ɵ�DA����ABE����һ���õ�ƽ��ABCD��ƽ��ABE������CB��AB����B����AEC����Ӱ���߶�EC�ϣ��ɵ�AE����BCE����BE?��BCE���õ�AE��EB��
������AΪԭ�㣬��ֱ��ƽ��ABCD��ֱ��Ϊx�ᣬAB����ֱ��Ϊy�ᣬADΪz�ᣬ��ͼ��ʾ�����ռ�ֱ������ϵA-xyz������֪$\frac{AF}{BG}$=��=$\frac{AE}{BE}$��������ڦˣ�ʹ�����B-AC-E������ֵΪ$\frac{\sqrt{3}}{3}$���ֱ����ƽ��AEC��ƽ��BAC��һ����������|cos��$\overrightarrow{m}��\overrightarrow{n}$��|=$\frac{\sqrt{3}}{3}$��a2=b2������$\overrightarrow{AE}•\overrightarrow{BE}=0$����a2+b��b-2��=0���������bֵ���ɵ�AE=BE��������=1ʱ�������B-AC-E������ֵΪ$\frac{{\sqrt{3}}}{3}$��
��� ����֤��������֪���ı���ABCD�DZ߳�Ϊ2�������Σ�
��DA��AF��DA��AE��AE��AF=A��
��DA����ABE����ƽ��ABCD��ƽ��ABE��
��CB��AB����CB��AE��
�ֵ�B����AEC����Ӱ���߶�EC�ϣ���ΪH����AE��BH��
��AE����BCE����BE?��BCE��
��AE��EB��
���⣺��AΪԭ�㣬��ֱ��ƽ��ABCD��ֱ��Ϊx�ᣬAB����ֱ��Ϊy�ᣬADΪz�ᣬ
��ͼ��ʾ�����ռ�ֱ������ϵA-xyz��
����֪$\frac{AF}{BG}$=��=$\frac{AE}{BE}$��������ڦˣ�ʹ�����B-AC-E������ֵΪ$\frac{\sqrt{3}}{3}$��
��E��a��b��0������$\overrightarrow{AE}=��a��b��0��$��$\overrightarrow{AC}=��0��2��2��$��
��ƽ��AEC��һ��������$\overrightarrow{n}=��x��y��z��$��
��$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=ax+by=0}\\{\overrightarrow{n}•\overrightarrow{AC}=2y+2z=0}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-\frac{b}{a}y}\\{z=-y}\end{array}\right.$��
��y=a����$\overrightarrow{n}=��-b��a��-a��$��ƽ��EAC��һ����������
��ƽ��BAC��һ��������Ϊ$\overrightarrow{m}=��1��0��0��$��
��|cos��$\overrightarrow{m}��\overrightarrow{n}$��|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=$\frac{|b|}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{3}}{3}$�������a2=b2 �٣�
�֡�AE��ƽ��BCE����AE��BE��
��$\overrightarrow{AE}•\overrightarrow{BE}=0$����a2+b��b-2��=0 �ڣ�
�����٢ڣ����b=0���ᣩ��b=1��
��$AE=\sqrt{{a}^{2}+{b}^{2}}$��BE=$\sqrt{{a}^{2}+��b-2��^{2}}$����AE=BE��
�൱��=1ʱ�������B-AC-E������ֵΪ$\frac{{\sqrt{3}}}{3}$��
���� ���⿼��ֱ����ƽ�洹ֱ���ж������ʣ�����ռ�����������˼ά������ѵ�������ÿռ�ֱ������ϵ������ǵ�ƽ��ǣ����е��⣮

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| A�� | $\frac{1}{2}$��$\frac{��}{6}$ | B�� | 1��$\frac{��}{6}$ | C�� | 1��$\frac{��}{3}$ | D�� | $\frac{1}{2}$��$\frac{��}{3}$ |
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
 ��ͼ����������ABCD-A1B1C1D1�У�E��CC1���е㣬��֤��
��ͼ����������ABCD-A1B1C1D1�У�E��CC1���е㣬��֤��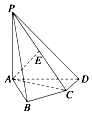 ��ͼ��������P-ABCD�У�PA�͵���ABCD��AB��AD��AC��CD����ABC=60�㣬PA=AB=BC��E��PC���е㣮
��ͼ��������P-ABCD�У�PA�͵���ABCD��AB��AD��AC��CD����ABC=60�㣬PA=AB=BC��E��PC���е㣮