题目内容
已知A={x|x2-1=0},B={y|y2-2ay+b=0,y∈R},若非空集合B⊆A,求实数a、b的值.
考点:集合的包含关系判断及应用
专题:集合
分析:由x2-1=0,解得x.可得A={-1,1}.由于非空集合B⊆A,可得B={-1},{1},{-1,1}.分类讨论利用一元二次方程根与系数的关系、与判别式的关系即可得出.
解答:
解:由x2-1=0,解得x=±1.∴A={-1,1}.
∵非空集合B⊆A,∴B={-1},{1},{-1,1}.
若B={-1,1},则
,解得a=0,b=-1.
若B只含一个元素-1或1,即B={-1},或{1}.
则△=4a2-4b=0,
∴
或
,
解得
或
.
综上可得:
或
或
.
∵非空集合B⊆A,∴B={-1},{1},{-1,1}.
若B={-1,1},则
|
若B只含一个元素-1或1,即B={-1},或{1}.
则△=4a2-4b=0,
∴
|
|
解得
|
|
综上可得:
|
|
|
点评:本题考查了一元二次方程根与系数的关系、与判别式的关系,可怜虫集合之间的关系,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
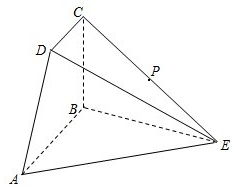 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.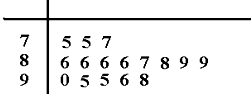 某统计部门用“10分制”调查一社区人们对物业管理的“满意度”.现从调查人群中随机抽取16名,以下茎叶图记录了他们的“满意度”分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某统计部门用“10分制”调查一社区人们对物业管理的“满意度”.现从调查人群中随机抽取16名,以下茎叶图记录了他们的“满意度”分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):