题目内容
 如图,在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PAC的体积.若f(M)=(
如图,在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PAC的体积.若f(M)=(| 1 |
| 2 |
| 1 |
| x |
| a |
| y |
考点:基本不等式,棱锥的结构特征
专题:不等式的解法及应用,空间位置关系与距离
分析:在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.可得三棱锥的体积VP-ABC=
SPAB•PC=1.得到4x+2y=1.利用基本不等式可得
+
=(4x+2y)(
+
)=4+2a+
+
≥4+2a+4
,当且仅当y=2
x取等号.又
+
≥8恒成立,4+2a+4
≥8,解得a≥6-4
.
| 1 |
| 3 |
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| 2y |
| x |
| 4ax |
| y |
| 2a |
| a |
| 1 |
| x |
| a |
| y |
| 2a |
| 2 |
解答:
解:在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.
∴VP-ABC=
SPAB•PC=
×
×3×2×1=1.
∴
+2x+y=1,化为4x+2y=1.
∵a>0,x>0,y>0.
∴
+
=(4x+2y)(
+
)=4+2a+
+
≥4+2a+2
=4+2a+4
,当且仅当y=2
x取等号.
又
+
≥8恒成立,∴4+2a+4
≥8,解得a≥6-4
.
故a的最小值是6-4
.
故答案为:6-4
.
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∵a>0,x>0,y>0.
∴
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| 2y |
| x |
| 4ax |
| y |
|
| 2a |
| a |
又
| 1 |
| x |
| a |
| y |
| 2a |
| 2 |
故a的最小值是6-4
| 2 |
故答案为:6-4
| 2 |
点评:本题考查了三棱锥的体积、基本不等式的性质、恒成立问题的等价转化,属于难题.

练习册系列答案
相关题目
 从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )
从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )| A、3 | B、7 | C、9 | D、18 |
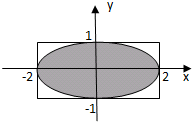 已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )
已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )| A、100个 | B、200个 |
| C、300个 | D、400个 |