题目内容
从区间[0,1]内任取两个数,则这两个数的和小于
的概率为 .
| 1 |
| 2 |
考点:几何概型
专题:概率与统计
分析:本题考查的知识点是几何概型的意义,关键是要找出[0,1]中随机地取出两个数所对应的平面区域的面积,及两数之和小于
对应的平面图形的面积大小,再代入几何概型计算公式,进行解答.
| 1 |
| 2 |
解答:
解:设取出两个数为x,y;则
,
若这两数之和小于
,则有
,
根据几何概型,原问题可以转化为求不等式组表示的区域
与
表示区域的面积之比问题,
如图所示;当两数之和小于
时,对应点落在阴影上,
∵S阴影=
×
×
=
,
故在区间[0,1]中随机地取出两个数,则两数之和小于
的概率P=
=
.
故答案为:
.
|

若这两数之和小于
| 1 |
| 2 |
|
根据几何概型,原问题可以转化为求不等式组表示的区域
|
|
如图所示;当两数之和小于
| 1 |
| 2 |
∵S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
故在区间[0,1]中随机地取出两个数,则两数之和小于
| 1 |
| 2 |
| ||
| 1×1 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若角α的终边过点P(3,-4),则cosα等于( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
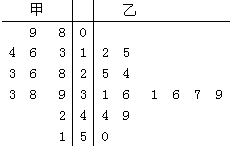 已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )| A、甲篮球运动员比赛得分更稳定,中位数为26 |
| B、甲篮球运动员比赛得分更稳定,中位数为27 |
| C、乙篮球运动员比赛得分更稳定,中位数为31 |
| D、乙篮球运动员比赛得分更稳定,中位数为36 |
 如图,在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PAC的体积.若
如图,在三棱锥P-ABC中PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PAC的体积.若