题目内容
椭圆
+
=1（b＞0）的焦距为2，则实数b的值为 ．
| x2 |
| 9 |
| y2 |
| b |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据椭圆方程的标准形式，结合焦距 2c=2，结合a，b，c的关系列出方程，从而求得b的值．
解答：
解：由椭圆
+
=1（b＞0）的焦距为2，得：
2c=2得c=1．
依题意得9-b=1或b-9=1
解得b=8或b=10，
故答案为：8或10
| x2 |
| 9 |
| y2 |
| b |
2c=2得c=1．
依题意得9-b=1或b-9=1
解得b=8或b=10，
故答案为：8或10
点评：本题是基础题，考查椭圆的标准方程、椭圆的简单性质，考查计算能力．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、在平面内共线的向量，在空间不一定共线 |
| B、在空间共线的向量，在平面内不一定共线 |
| C、在平面内共线的向量，在空间一定不共线 |
| D、在空间共线的向量，在平面内一定共线 |
已知抛物线C1：x2=4py，圆C2：x2+（y-p）2=p2，直线l：y=| 1 |
| 2 |
| AB |
| CD |
A、
| ||
B、
| ||
C、
| ||
| D、p2 |
函数y=
的定义域（ ）
| ||
| x |
| A、{x|x≠0} |
| B、（-4，+∞） |
| C、（-4，0）∪（0，+∞） |
| D、[-4，0）∪（0，+∞） |
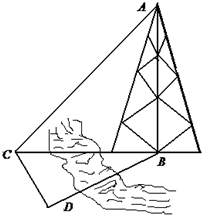如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C，D．现测得∠BCD=60°，∠DBC=45°，CD=20m，并在点C测得塔顶A的仰角为45°，求塔高AB（精确到0.1，